题目内容
某班级2014年元旦迎新有奖活动中有一节目,投掷一个各面分别有数字1,2,3,4,且质地均匀的小正四面体,记其底面的数字为投掷的点数,规定:参与者连续投掷三次,投出的点数全部一样,或只含有1、3,或只含有2、4,则获奖,如“4,4,4”,“1,1,3”,“2,2,4”等情形获奖,每人仅限参与节目一次.
(1)求参与者甲获奖的概率;
(2)获奖一次得到奖金10元,否则得到1元,求参与者甲、乙、丙三人总共获得的奖金ξ的分布列与数学期望.
(1)求参与者甲获奖的概率;
(2)获奖一次得到奖金10元,否则得到1元,求参与者甲、乙、丙三人总共获得的奖金ξ的分布列与数学期望.
考点:离散型随机变量的期望与方差,列举法计算基本事件数及事件发生的概率,离散型随机变量及其分布列
专题:概率与统计
分析:(1)甲连续投掷三次,基本事件总数n=43=64,投出的点数全部一样,或只含有1、3,或只含有2、4的种数m=23+23=16,由此能求出参与者甲获奖的概率.
(2)参与者甲、乙、丙三人获奖人数X~B(3,
),由题意知ξ的可能取值为3,12,21,30,由此能求出参与者甲、乙、丙三人总共获得的奖金ξ的分布列与数学期望.
(2)参与者甲、乙、丙三人获奖人数X~B(3,
| 1 |
| 4 |
解答:
解:(1)甲连续投掷三次,基本事件总数n=43=64,
投出的点数全部一样,或只含有1、3,或只含有2、4的种数m=23+23=16,
∴参与者甲获奖的概率p=
=
=
.
(2)由(1)知参与者甲、乙、丙获奖的概率均为
,且相互独立,
∴参与者甲、乙、丙三人获奖人数X~B(3,
),
由题意知ξ的可能取值为3,12,21,30,
P(ξ=3)=P(X=0)=
(
)3=
,
P(ξ=12)=P(X=1)=
(
)(
)2=
,
P(ξ=21)=P(X=2)=
(
)2(
)=
,
P(ξ=30)=P(X=4)=
(
)3=
,
∴ξ的分布列为:
Eξ=3×
+12×
+21×
+30×
=
.
投出的点数全部一样,或只含有1、3,或只含有2、4的种数m=23+23=16,
∴参与者甲获奖的概率p=
| m |
| n |
| 16 |
| 64 |
| 1 |
| 4 |
(2)由(1)知参与者甲、乙、丙获奖的概率均为
| 1 |
| 4 |
∴参与者甲、乙、丙三人获奖人数X~B(3,
| 1 |
| 4 |
由题意知ξ的可能取值为3,12,21,30,
P(ξ=3)=P(X=0)=
| C | 0 3 |
| 3 |
| 4 |
| 27 |
| 64 |
P(ξ=12)=P(X=1)=
| C | 1 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 27 |
| 64 |
P(ξ=21)=P(X=2)=
| C | 2 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 9 |
| 64 |
P(ξ=30)=P(X=4)=
| C | 3 3 |
| 1 |
| 4 |
| 1 |
| 64 |
∴ξ的分布列为:
| ξ | 3 | 12 | 21 | 30 | ||||||||
| P |
|
|
|
|
| 27 |
| 64 |
| 27 |
| 64 |
| 9 |
| 64 |
| 1 |
| 64 |
| 39 |
| 4 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
集合A={x|
≥2,x∈Z}的子集个数为( )
| x-1 |
| x+1 |
| A、2 | B、3 | C、4 | D、5 |
某几何体的三视图如图所示,那么该几何体的表面积为( )
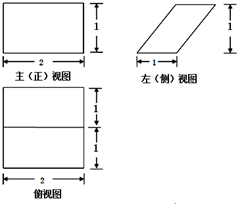

| A、2 | ||
| B、14 | ||
C、6+4
| ||
D、4+6
|
在棱长都相等的四面体ABCD中,M,N分别为BC,CD的中点,则MN与AC所成角为( )
| A、30° | B、45° |
| C、60° | D、90° |