题目内容

在△ABC中，已知
AB
=a，
AC
=b，D为BC边的中点，则下列向量与
AD
 同向的是（　　）
A、
a+b
|a+b|
B、
a
|a|
+
b
|b|
C、
a-b
|a-b|
D、
a
|a|
-
b
|b|
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：D为BC边的中点，利用向量的平行四边形法则可得
a
+
b
=2
AD
．即可得出．
解答： 解：∵D为BC边的中点，
∴
a
+
b
=2
AD
．
∴
a
+
b
|
a
+
b
|
与
AD
同方向．
故选：A．
点评：本题考查了向量的平行四边形法则、共线向量，属于基础题．
练习册系列答案
相关题目
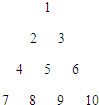设等比数列{an}的前n项和Sn=2•3n-2+a，等差数列{bn}的前n项和Tn=2n2-n+b-1，则a+b=
 
．
把正整数按上小下大、左小右大的原则排成如图三角形数表（每行比上一行多一个数）：设ai，j（i、j∈N*）是位于这个三角形数表中从上往下数第i行、从左往右数第j个数，如a4，2=8，则a51，25为
 
．
读右侧程序框图，该程序运行后输出的A值为
 
．
已知定义在R上的奇函数f（x）满足f（x+1）=f（x），当0＜x＜
1
2
时，f（x）=4x，则f（-
5
4
）=（　　）
A、-
2
B、-
2
2
C、-1
D、
2
2
下列说法正确的是（　　）
A、命题“若x2=1，则x=1”的否命题是“若x2=1，则x≠1”
B、“x=-1”是“x2-x-2=0”的必要不充分条件
C、“tanx=1”是“x=
π
4
”的充分不必要条件
D、命题“若x=y，则sinx=siny”的逆否命题是真命题
已知函数f（x）=ax+lnx（a∈R）．
（Ⅰ）若a=2，求曲线y=f（x）在x=1处的切线方程；
（Ⅱ）求f（x）的单调区间；
（Ⅲ）设g（x）=x2-2x+2，若对任意x1∈（0，+∞），均存在x2∈[0，1]，使得f（x1）＜g（x2），求a的取值范围．
定义在（0，+∞）上的函数f（x）满足：①当x∈[1，3）时，f（x）=1-|x-2|；②f（3x）=3f（x）．设关于x的函数F（x）=f（x）-a的零点从小到大依次为x1，x2，…，xn，…（n∈N*）．若a∈（1，3），则x1+x2+…+x2n-1+x2n=
 
．（用n表示）
命题“?x∈[-∞，0），x3+x≥0”的否定是（　　）
A、?x∈[-∞，0），x3+x＜0
B、?x∈（-∞，0），x3+x≥0
C、?x0∈[0，+∞），x03+x0＜0
D、?x0∈[0，+∞），x03+x0≥0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网