题目内容
已知函数f(x)=ax+lnx(a∈R).
(Ⅰ)若a=2,求曲线y=f(x)在x=1处的切线方程;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=x2-2x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.
(Ⅰ)若a=2,求曲线y=f(x)在x=1处的切线方程;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=x2-2x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(Ⅰ)把a的值代入f(x)中,求出f(x)的导函数,把x=1代入导函数中求出的导函数值即为切线的斜率,可得曲线y=f(x)在x=1处的切线方程;
(Ⅱ)求出f(x)的导函数,分a大于等于0和a小于0两种情况讨论导函数的正负,进而得到函数的单调区间;
(Ⅲ)对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),等价于f(x)max<g(x)max,分别求出相应的最大值,即可求得实数a的取值范围.
(Ⅱ)求出f(x)的导函数,分a大于等于0和a小于0两种情况讨论导函数的正负,进而得到函数的单调区间;
(Ⅲ)对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),等价于f(x)max<g(x)max,分别求出相应的最大值,即可求得实数a的取值范围.
解答:
解:(Ⅰ)由已知f′(x)=2+
(x>0),f'(1)=2+1=3,所以斜率k=3,
又切点(1,2),所以切线方程为y-2=3(x-1)),即3x-y-1=0
故曲线y=f(x)在x=1处切线的切线方程为3x-y-1=0.-----------------(4分)
(Ⅱ)f′(x)=a+
=
(x>0)
①当a≥0时,由于x>0,故ax+1>0,f'(x)>0,所以f(x)的单调递增区间为(0,+∞).------(6分)
②当a<0时,由f'(x)=0,得x=-
.
在区间(0,-
)上,f'(x)>0,在区间(-
,+∞)上,f'(x)<0,
所以,函数f(x)的单调递增区间为(0,-
),单调递减区间为(-
,+∞).--------(8分)
(Ⅲ)由已知,转化为f(x)max<g(x)max.g(x)=(x-1)2+1,x∈[0,1],所以g(x)max=2
由(Ⅱ)知,当a≥0时,f(x)在(0,+∞)上单调递增,值域为R,故不符合题意.
(或者举出反例:存在f(e3)=ae3+3>2,故不符合题意.)
当a<0时,f(x)在(0,-
)上单调递增,在(-
,+∞)上单调递减,
故f(x)的极大值即为最大值,f(-
)=-1+ln(-
)=-1-ln(-a),
所以2>-1-ln(-a),解得a<-
.-----------------------(12分)
| 1 |
| x |
又切点(1,2),所以切线方程为y-2=3(x-1)),即3x-y-1=0
故曲线y=f(x)在x=1处切线的切线方程为3x-y-1=0.-----------------(4分)
(Ⅱ)f′(x)=a+
| 1 |
| x |
| ax+1 |
| x |
①当a≥0时,由于x>0,故ax+1>0,f'(x)>0,所以f(x)的单调递增区间为(0,+∞).------(6分)
②当a<0时,由f'(x)=0,得x=-
| 1 |
| a |
在区间(0,-
| 1 |
| a |
| 1 |
| a |
所以,函数f(x)的单调递增区间为(0,-
| 1 |
| a |
| 1 |
| a |
(Ⅲ)由已知,转化为f(x)max<g(x)max.g(x)=(x-1)2+1,x∈[0,1],所以g(x)max=2
由(Ⅱ)知,当a≥0时,f(x)在(0,+∞)上单调递增,值域为R,故不符合题意.
(或者举出反例:存在f(e3)=ae3+3>2,故不符合题意.)
当a<0时,f(x)在(0,-
| 1 |
| a |
| 1 |
| a |
故f(x)的极大值即为最大值,f(-
| 1 |
| a |
| 1 |
| a |
所以2>-1-ln(-a),解得a<-
| 1 |
| e3 |
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导数研究函数的单调性,掌握不等式恒成立时所满足的条件,是一道中档题.

练习册系列答案
相关题目
在△ABC中,已知
=a,
=b,D为BC边的中点,则下列向量与
同向的是( )
| AB |
| AC |
| AD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列1,-3,5,-7,9,…的一个通项公式{an}=( )
| A、2n-1 |
| B、(-1)n(2n+1) |
| C、(-1)n(2n-1) |
| D、(-1)n+1(2n-1) |
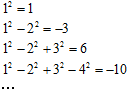
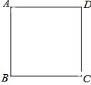 如图,在正方形ABCD中,求正方形内一点到A,B,D的距离和最短.
如图,在正方形ABCD中,求正方形内一点到A,B,D的距离和最短.