题目内容
定义在(0,+∞)上的函数f(x)满足:①当x∈[1,3)时,f(x)=1-|x-2|;②f(3x)=3f(x).设关于x的函数F(x)=f(x)-a的零点从小到大依次为x1,x2,…,xn,…(n∈N*).若a∈(1,3),则x1+x2+…+x2n-1+x2n= .(用n表示)
考点:分段函数的应用
专题:函数的性质及应用
分析:根据分段函数的表达式,作出函数的图象,利用数形结合确定零点的取值关系,利用数列求和的公式即可得到结论.
解答:
解:由①当x∈[1,3)时,f(x)=1-|x-2|=
,
可画出f(x)在[1,3)上的图象,根据②f(3x)=3f(x),只要将f(x)在[1,3)上的图象沿x轴伸长到原来的3倍,
再沿y轴伸长到原来的3倍即可得到f(x)在[3,9)上的图象,
以此类推,可得到在[9,27),[27,81)…上的图象,
关于x的函数F(x)=f(x)-a的零点,可看成函数y=f(x)与y=a图象交点的横坐标,由函数y=f(x)图象的对称性可知:
=6,
=6×3,
=6×32,…如图,
所以就有
(x1+x2+…+x2n-1+x2n)=6+6×3+6×32+…+6×3n-1=
=3(3n-1),
因此x1+x2+…+x2n-1+x2n=6(3n-1)

|
可画出f(x)在[1,3)上的图象,根据②f(3x)=3f(x),只要将f(x)在[1,3)上的图象沿x轴伸长到原来的3倍,
再沿y轴伸长到原来的3倍即可得到f(x)在[3,9)上的图象,
以此类推,可得到在[9,27),[27,81)…上的图象,
关于x的函数F(x)=f(x)-a的零点,可看成函数y=f(x)与y=a图象交点的横坐标,由函数y=f(x)图象的对称性可知:
| x1+x2 |
| 2 |
| x3+x4 |
| 2 |
| x5+x6 |
| 2 |
所以就有
| 1 |
| 2 |
| 6(1-3n) |
| 1-3 |
因此x1+x2+…+x2n-1+x2n=6(3n-1)

点评:本题主要考查函数图象与性质及等比数列求和.综合性较强难度较大,利用数形结合是解决本题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
在△ABC中,已知
=a,
=b,D为BC边的中点,则下列向量与
同向的是( )
| AB |
| AC |
| AD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列1,-3,5,-7,9,…的一个通项公式{an}=( )
| A、2n-1 |
| B、(-1)n(2n+1) |
| C、(-1)n(2n-1) |
| D、(-1)n+1(2n-1) |
已知复数z满足(1-i)z=2,则z=( )
| A、-1-i | B、-1+i |
| C、1-i | D、1+i |
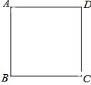 如图,在正方形ABCD中,求正方形内一点到A,B,D的距离和最短.
如图,在正方形ABCD中,求正方形内一点到A,B,D的距离和最短.