题目内容
已知定义在R上的奇函数f(x)满足f(x+1)=f(x),当0<x<
时,f(x)=4x,则f(-
)=( )
| 1 |
| 2 |
| 5 |
| 4 |
A、-
| ||||
B、-
| ||||
| C、-1 | ||||
D、
|
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数的奇函数得f(-
)=-f(
),再根据f(x+1)=f(x),把)=-f(
)=-f(
+1)=-f(
),进而求解.
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:因为函数的奇函数,
所以f(-
)=-f(
)
又f(
+1)=f(
)=4
=
,
所以f(-
)=-
.
故选A.
所以f(-
| 5 |
| 4 |
| 5 |
| 4 |
又f(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
所以f(-
| 5 |
| 4 |
| 2 |
故选A.
点评:本题主要考查奇函数的性质、分段函数的性质,属于基础题.

练习册系列答案
相关题目
在△ABC中,已知
=a,
=b,D为BC边的中点,则下列向量与
同向的是( )
| AB |
| AC |
| AD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列判断错误的是( )
| A、“am2<bm2”是“a<b“的充分不必要条件 | ||||
| B、命题“?∈R,x3-x2-1≤0”的否定是“?x∈R,x3-x2-1>0” | ||||
C、命题“若α=
| ||||
| D、若p∧q为假命题,则p,q均为假命题 |




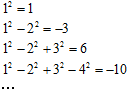
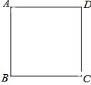 如图,在正方形ABCD中,求正方形内一点到A,B,D的距离和最短.
如图,在正方形ABCD中,求正方形内一点到A,B,D的距离和最短.