题目内容
设等比数列{an}的前n项和Sn=2•3n-2+a,等差数列{bn}的前n项和Tn=2n2-n+b-1,则a+b= .
考点:数列的求和
专题:等差数列与等比数列
分析:由给出的等比数列和等差数列的前n项和求通项,结合n=1时适合n≥2时的通项公式求得a,b的值,则答案可求.
解答:
解:由Sn=2•3n-2+a,得
a1=
+a,
an=Sn-Sn-1=4•3n-3(n≥2),
∵数列{an}是等比数列,
∴
+a=
,a=-
;
由Tn=2n2-n+b-1,得
b1=b,
bn=Tn-Tn-1=4n-3(n≥2),
∵数列{bn}是等差数列,
∴b=1.
∴a+b=-
+1=
.
故答案为:
.
a1=
| 2 |
| 3 |
an=Sn-Sn-1=4•3n-3(n≥2),
∵数列{an}是等比数列,
∴
| 2 |
| 3 |
| 4 |
| 9 |
| 2 |
| 9 |
由Tn=2n2-n+b-1,得
b1=b,
bn=Tn-Tn-1=4n-3(n≥2),
∵数列{bn}是等差数列,
∴b=1.
∴a+b=-
| 2 |
| 9 |
| 7 |
| 9 |
故答案为:
| 7 |
| 9 |
点评:本题考查了由数列的和求数列的通项公式,考查了等差关系和等比关系的确定,是中档题.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
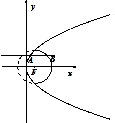 如图所示,直线y=m与抛物线y2=8x交与点A,与圆(x-2)2+y2=16的实线部分交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )
如图所示,直线y=m与抛物线y2=8x交与点A,与圆(x-2)2+y2=16的实线部分交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )| A、(6,8) |
| B、(4,6) |
| C、(8,12) |
| D、(8,10) |
在△ABC中,已知
=a,
=b,D为BC边的中点,则下列向量与
同向的是( )
| AB |
| AC |
| AD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|