题目内容
在△ABC中,A=
且三个内角的正弦值成等比数列,则其最小角的正弦值( )
| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:正弦定理
专题:解三角形
分析:由在△ABC中,A=
且三个内角的正弦值成等比数列,利用等比数列的性质列出关系式,把sinA=1,sinC=cosB代入求出sinB的值即可.
| π |
| 2 |
解答:
解:设最小的角为B,根据题意得:sin2C=sinAsinB,
把sinA=1,sinC=cosB代入得:cos2B=sinB,即sin2B+sinB-1=0,
解得:sinB=
或sinB=
(舍去),
则其最小角的正弦值为
,
故选:B.
把sinA=1,sinC=cosB代入得:cos2B=sinB,即sin2B+sinB-1=0,
解得:sinB=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
则其最小角的正弦值为
| ||
| 2 |
故选:B.
点评:此题考查了正弦定理,等比数列的性质,以及特殊角的三角函数值,熟练掌握等比数列的性质是解本题的关键.

练习册系列答案
相关题目
命题“若x>2,则x>1”的逆命题是( )
| A、若x>1,则x>2 |
| B、若x≤2,则x≤1 |
| C、若x≤1,则x≤2 |
| D、若x<2,则x<1 |
已知集合A={x|x>0},则命题“任意x∈A,x2-|x|>0”的否定是( )
| A、任意x∈A,x2-|x|≤0 |
| B、任意x∉A,x2-|x|≤0 |
| C、存在x∉A,x2-|x|>0 |
| D、存在x∈A,x2-|x|≤0 |
已知函数f(x-1)是定义在R上的奇函数,若对于任意两个实数x1≠x2,不等式
>0恒成立,则不等式f(x+3)<0的解集为( )
| f(x1)-f(x2) |
| x1-x2 |
| A、(-∞,-3) |
| B、(4,+∞) |
| C、(-∞,1) |
| D、(-∞,-4) |
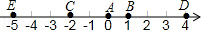 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样移动解答:
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样移动解答: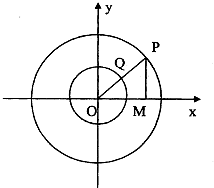 以原点为圆心的两个同心圆的方程分别为x2+y2=4和x2+y2=1,过原点O的射线交大圆于点P,交小圆于点Q,作PM⊥x轴于M,若
以原点为圆心的两个同心圆的方程分别为x2+y2=4和x2+y2=1,过原点O的射线交大圆于点P,交小圆于点Q,作PM⊥x轴于M,若