Question

四面体的六条棱中，有五条棱长都等于a，当四面体的体积最大时，其表面积为

 

．

Answer 1

考点：组合几何体的面积、体积问题

专题：计算题,空间位置关系与距离

分析：判断几何体体积最大时的结构特征，然后利用四面体的表面积就是表面四个三角形的面积和，可直接运用三角形的面积求解．

解答： 解：△ABC和△BCD都是边长为a的正三角形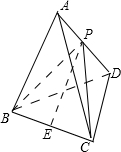，三棱锥的体积的最大值，是A到底面的距离最大时取得，就是侧面ABC与底面BCD垂直时取得最大值．此时
△ABD和△ACD是全等的等腰三角形，其腰长为a，底边长为

6

2

a，
∴S_△ABC=S_△BCD=

1

2

a×

3

2

a=

3

4

a2，
S_△ABD=S_△ACD=

1

2

×

6

2

a×

a2- 3 8 a2

=

15

8

a2，
∴当四面体的体积最大时，其表面积S=

3

4

a2+

15

8

a2．
故答案为：

3

4

a2+

15

8

a2．

点评：本题考查了棱锥的体积和表面积，考查了学生的空间想象能力和数学转化能力，考查了函数思想，运用了基本不等式求函数的最值，此题是中档题．