题目内容
已知函数f(x)=
,g(x)=|x-
|.
(1)a=-2时,求函数g(x)的最小值;
(2)若对?t∈[1,3],在区间[1,3]总存在两个不同的x,使得g(x)=f(t),求实数a的取值范围.
| x+3 |
| x+1 |
| a |
| x |
(1)a=-2时,求函数g(x)的最小值;
(2)若对?t∈[1,3],在区间[1,3]总存在两个不同的x,使得g(x)=f(t),求实数a的取值范围.
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(1)当a=-2时,g(x)=|x+
|=|x|+|
|,利用基本不等式求最小值;
(2)当t∈[1,3]时,f(t)=1+
∈[
,2];故对?t∈[1,3],在区间[1,3]总存在两个不同的x,使得g(x)=f(t)可化为方程g(x)=m,当m∈[
,2]时,在x∈[1,3]上有两个不同的根,从而讨论求解.
| 2 |
| x |
| 2 |
| x |
(2)当t∈[1,3]时,f(t)=1+
| 2 |
| t+1 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:(1)当a=-2时,g(x)=|x+
|=|x|+|
|≥2
;
(当且仅当x=±
时,等号成立);
故函数的最小值为2
;
(2)当t∈[1,3]时,f(t)=1+
∈[
,2];
故对?t∈[1,3],在区间[1,3]总存在两个不同的x,使得g(x)=f(t)可化为
方程g(x)=m,当m∈[
,2]时,在x∈[1,3]上有两个不同的根,
①当a=0时,g(x)=|x|,在[1,3]上单调递增,舍去;
②当a>0时,g(x)在(0,
)上单调递减,在(
,+∞)上单调递增;
则
;
解得,a=3;
③当a<0时,g(x)在(0,
)上单调递减,在(
,+∞)上单调递增;
则
;无解;
综上所述,a=3.
| 2 |
| x |
| 2 |
| x |
| 2 |
(当且仅当x=±
| 2 |
故函数的最小值为2
| 2 |
(2)当t∈[1,3]时,f(t)=1+
| 2 |
| t+1 |
| 3 |
| 2 |
故对?t∈[1,3],在区间[1,3]总存在两个不同的x,使得g(x)=f(t)可化为
方程g(x)=m,当m∈[
| 3 |
| 2 |
①当a=0时,g(x)=|x|,在[1,3]上单调递增,舍去;
②当a>0时,g(x)在(0,
| a |
| a |
则
|
解得,a=3;
③当a<0时,g(x)在(0,
| -a |
| -a |
则
|
综上所述,a=3.
点评:本题考查了绝对值函数的最值的求法,同时考查了基本不等式的应用及恒成立问题,属于中档题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
设抛物线W:y2=4x的焦点为F,过F的直线与W相交于A,B两点,记点F到直线l:x=-1的距离为d,则有( )
| A、|AB|≥2d |
| B、|AB|=2d |
| C、|AB|≤2d |
| D、|AB|<2d |
函数f(x)=ln(x+2)-
的零点所在区间为(k,k+1)(其中k为整数),则k的值为( )
| 1 |
| x |
| A、0 | B、1 | C、-2 | D、0或-2 |
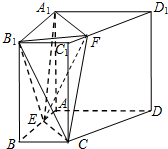 如图,在四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,∠BAD=90°,AD∥BC,且A1A=AB=AD=2BC=2,点E在棱AB上,平面A1EC与棱C1D1相交于点F.
如图,在四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,∠BAD=90°,AD∥BC,且A1A=AB=AD=2BC=2,点E在棱AB上,平面A1EC与棱C1D1相交于点F.