题目内容
已知圆O的方程为x2+y2=4.
(1)求过点P(1,2)且与圆O相切的直线l的方程;
(2)直线m过点P(1,2),且与圆O交于A、B两点,若|AB|=2
,求直线m的方程;
(3)圆O上有一动点M(x0,y0),
=(2x0,y0),若向量
=2
+
,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
(1)求过点P(1,2)且与圆O相切的直线l的方程;
(2)直线m过点P(1,2),且与圆O交于A、B两点,若|AB|=2
| 3 |
(3)圆O上有一动点M(x0,y0),
| ON |
| OQ |
| OM |
| 1 |
| 2 |
| ON |
考点:轨迹方程,直线与圆的位置关系
专题:圆锥曲线的定义、性质与方程
分析:(1)设出过点P(1,2)的直线方程,利用直线与圆O相切的推出关系式,即可求出直线方程;
(2)通过直线m与x轴垂直,与不垂直,两种情况,利用圆心距半径半弦长关系,即可求直线m的方程;
(3)设Q点的坐标为(x,y),圆O上有一动点M(x0,y0),通过
=(2x0,y0),以及
=2
+
,得到Q,M点的关系,通过M在圆上,即可求动点Q的轨迹方程,然后说明此轨迹是椭圆.
(2)通过直线m与x轴垂直,与不垂直,两种情况,利用圆心距半径半弦长关系,即可求直线m的方程;
(3)设Q点的坐标为(x,y),圆O上有一动点M(x0,y0),通过
| ON |
| OQ |
| OM |
| 1 |
| 2 |
| ON |
解答:
解 (1)显然直线l的斜率存在,设切线方程为y-2=k(x-1),
则由
=2,得k1=0,k2=-
,
从而所求的切线方程为y=2和4x+3y-10=0.
(2)当直线m垂直于x轴时,此时直线方程为x=1,m与圆的两个交点坐标为(1,
)和
(1,-
),这两点的距离为2
,满足题意;当直线m不垂直于x轴时,设其方程为
y-2=k(x-1),即kx-y-k+2=0,设圆心到此直线的距离为d(d>0),
则2
=2
,得d=1,从而1=
,得k=
,此时直线方程为3x-4y+5=0,综上所述,所求直线m的方程为3x-4y+5=0或x=1.
(3)设Q点的坐标为(x,y),M点坐标是(x0,y0),
=(2x0,y0),
∵
=2
+
,
∴(x,y)=(2x0,2y0)+(x0,
y0)=(3x0,
y0)⇒x0=
x,y0=
y
.∵x02+y02=4,∴(
x)2+(
y)2=4,即
+
=1.
∴Q点的轨迹方程是
+
=1,轨迹是一个焦点在x轴上的椭圆.
则由
| |2-k| | ||
|
| 4 |
| 3 |
从而所求的切线方程为y=2和4x+3y-10=0.
(2)当直线m垂直于x轴时,此时直线方程为x=1,m与圆的两个交点坐标为(1,
| 3 |
(1,-
| 3 |
| 3 |
y-2=k(x-1),即kx-y-k+2=0,设圆心到此直线的距离为d(d>0),
则2
| 3 |
| 4-d2 |
| |-k+2| | ||
|
| 3 |
| 4 |
(3)设Q点的坐标为(x,y),M点坐标是(x0,y0),
| ON |
∵
| OQ |
| OM |
| 1 |
| 2 |
| ON |
∴(x,y)=(2x0,2y0)+(x0,
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 3 |
| 2 |
| 5 |
.∵x02+y02=4,∴(
| 1 |
| 3 |
| 2 |
| 5 |
| x2 |
| 36 |
| y2 |
| 25 |
∴Q点的轨迹方程是
| x2 |
| 36 |
| y2 |
| 25 |
点评:本题考查轨迹方程的求法,直线与圆的位置关系的应用,考查转化思想以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知偶函数f(x)满足f(-1)=0,且在区间[0,+∞)上为减函数,不等式f(log2x)>0的解集为( )
| A、(-1,1) | ||
| B、(-∞,-1)∪(1,+∞) | ||
C、(
| ||
D、(0,
|
设y1=40.9,y2=80.5,y3=(
)-1.6,则( )
| 1 |
| 2 |
| A、y3>y1>y2 |
| B、y2>y1>y3 |
| C、y1>y2>y3 |
| D、y1>y3>y2 |
在等差数列{an}中,a3+a5=10,a7=2,则a1=( )
| A、5 | B、8 | C、10 | D、14 |
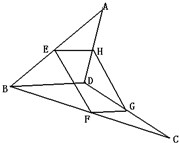 如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,求证:BD∥面EFGH.
如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,求证:BD∥面EFGH.