题目内容
设函数f(x)=cosx+sinx,问是否存在α∈(0,
),使f(x+α)=f(x+3α)恒成立?证明你的结论.
| π |
| 2 |
考点:两角和与差的正弦函数,正弦函数的定义域和值域
专题:计算题,函数的性质及应用
分析:运用两角和的正弦公式化简f(x),得到函数的周期性,假设存在α∈(0,
),使f(x+α)=f(x+3α)恒成立,则f(x+2α)=f(x),即有f(x)的最小正周期为2α,令α=π,即可判断.
| π |
| 2 |
解答:
解:函数f(x)=cosx+sinx
=
(
cosx+
sinx)
=
sin(x+
),
则函数f(x)的最小正周期为2π,
假设存在α∈(0,
),使f(x+α)=f(x+3α)恒成立,
则f(x)=f(x-α+3α)即有f(x+2α)=f(x),
即有f(x)的最小正周期为2α,
即2π=2α,即α=π,这与α∈(0,
)矛盾,
故不存在α∈(0,
),使f(x+α)=f(x+3α)恒成立.
=
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 2 |
| π |
| 4 |
则函数f(x)的最小正周期为2π,
假设存在α∈(0,
| π |
| 2 |
则f(x)=f(x-α+3α)即有f(x+2α)=f(x),
即有f(x)的最小正周期为2α,
即2π=2α,即α=π,这与α∈(0,
| π |
| 2 |
故不存在α∈(0,
| π |
| 2 |
点评:本题考查三角函数的化简和周期性,考查存在性问题的解决方法,属于中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
若复数z=(
)2014,则ln|z|=( )
| 1+i |
| 1-i |
| A、-2 | B、0 | C、1 | D、不存在 |
下列各式中正确的个数是( )
①0∈{0};②0∈∅;③∅?{0}④∅={0}.
①0∈{0};②0∈∅;③∅?{0}④∅={0}.
| A、1个 | B、2个 | C、3个 | D、4个 |
定义在R上的奇函数f(x),满足f(x)=f(x-3),f(-2)=0,则f(x)在区间(0,6)内零点个数( )
| A、至多4个 | B、至多5个 |
| C、恰好6个 | D、至少6个 |
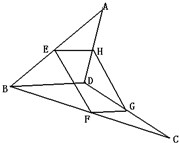 如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,求证:BD∥面EFGH.
如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,求证:BD∥面EFGH.