题目内容
函数f（x）=x2-2mx与g（x）=
在区间[1，2]上都是减函数，则m的取值范围是（ ）
| mx+3 |
| x+1 |
| A、[2，3） |
| B、[2，3] |
| C、[2，+∞） |
| D、（-∞，3） |
考点：函数单调性的性质
专题：函数的性质及应用
分析：结合二次函数的图象和性质可得若函数f（x）在区间[1，2]上都是减函数，则m≥2，结合反比例函数的图象和性质可得：若函数g（x）在区间[1，2]上是减函数，则3-m＞0，进而得到答案．
解答：
解：∵f（x）=x2-2mx的图象是开口向上，且以直线x=m为对称轴的抛物线，
故f（x）=x2-2mx在（-∞，m]上为减函数，
若函数f（x）在区间[1，2]上都是减函数，则m≥2，
又∵g（x）=
=
+m，
若函数g（x）在区间[1，2]上是减函数，则3-m＞0，则m＜3，
故m的取值范围是[2，3），
故选：A
故f（x）=x2-2mx在（-∞，m]上为减函数，
若函数f（x）在区间[1，2]上都是减函数，则m≥2，
又∵g（x）=
| mx+3 |
| x+1 |
| 3-m |
| x+1 |
若函数g（x）在区间[1，2]上是减函数，则3-m＞0，则m＜3，
故m的取值范围是[2，3），
故选：A
点评：本题考查的知识点是函数单调性的性质，熟练掌握二次函数和反比例函数的图象和性质是解答的关键．
练习册系列答案
相关题目
定义在R上的奇函数f（x），满足f（x）=f（x-3），f（-2）=0，则f（x）在区间（0，6）内零点个数（ ）
| A、至多4个 | B、至多5个 |
| C、恰好6个 | D、至少6个 |
已知偶函数f（x）满足f（-1）=0，且在区间[0，+∞）上为减函数，不等式f（log2x）＞0的解集为（ ）
| A、（-1，1） | ||
| B、（-∞，-1）∪（1，+∞） | ||
C、(
| ||
D、(0，
|
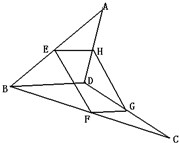如图，四边形EFGH为空间四边形ABCD的一个截面，若截面为平行四边形，求证：BD∥面EFGH．
某公司从一批产品中随机抽出60件进行检测．如图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100），[100，102），[102，104），[104，106]．