题目内容
已知圆C方程为(x-3)2+y2=12,定点A(-3,0),P是圆上任意一点,线段AP的垂直平分线l和直线CP相交于点Q.
(Ⅰ)当点P在圆上运动时,求点Q的轨迹E的方程.
(Ⅱ)过点C倾斜角为30°的直线交曲线E于A、B两点,求|AB|.
(Ⅰ)当点P在圆上运动时,求点Q的轨迹E的方程.
(Ⅱ)过点C倾斜角为30°的直线交曲线E于A、B两点,求|AB|.
考点:轨迹方程,直线与圆锥曲线的关系
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由题意可得点Q满足双曲线的定义,且求得a,c的值,再由b2=c2-a2求得b,则点Q的轨迹E的方程可求;
(Ⅱ)由题意得到直线AB的方程,和双曲线方程联立后利用弦长公式得答案.
(Ⅱ)由题意得到直线AB的方程,和双曲线方程联立后利用弦长公式得答案.
解答:
解:(Ⅰ)由点Q是线段AP垂直平分线上的点,
∴|AQ|=|PQ|,
又∵|QA|-|QC|=|PC|=2
<|AC|=6,
满足双曲线的定义.
设E的方程为
-
=1(a>0,b>0),
则a=
,c=3,
b=
=
,
则轨迹E方程为
-
=1;
(Ⅱ)直线AB的倾斜角为30°,且直线过C(3,0),
∴y=
(x-3)直线AB的方程为y=
(x-3),
由
,消去y得5x2+6x-27=0,
设A(x1,y1),B(x2,y2),
∴有x1+x2=-
,x1x2=-
.
则|AB|=
•
=
.
∴|AQ|=|PQ|,
又∵|QA|-|QC|=|PC|=2
| 3 |
满足双曲线的定义.
设E的方程为
| x2 |
| a2 |
| y2 |
| b2 |
则a=
| 3 |
b=
| c2-a2 |
| 6 |
则轨迹E方程为
| x2 |
| 3 |
| y2 |
| 6 |
(Ⅱ)直线AB的倾斜角为30°,且直线过C(3,0),
∴y=
| ||
| 3 |
| ||
| 3 |
由
|
设A(x1,y1),B(x2,y2),
∴有x1+x2=-
| 6 |
| 5 |
| 27 |
| 5 |
则|AB|=
1+(
|
(-
|
| 16 |
| 5 |
| 3 |
点评:本题考查了轨迹方程的求法,考查了直线与圆锥曲线的关系,涉及直线与圆锥曲线的关系问题,常用根与系数的关系解决,是压轴题.

练习册系列答案
相关题目
下列命题中,
①若
与
互为相反向量,则
+
=0;
②若k为实数,且k•
=
,则
=
或k=0;
③若
•
=0,则
=0或
=0;
④若
与
为平行的向量,则
•
=|
|•|
|;
⑤若|
|=1,则
=±1.
其中假命题的个数为( )
①若
| a |
| b |
| a |
| b |
②若k为实数,且k•
| a |
| 0 |
| a |
| 0 |
③若
| a |
| b |
| a |
| b |
④若
| a |
| b |
| a |
| b |
| a |
| b |
⑤若|
| a |
| a |
其中假命题的个数为( )
| A、5个 | B、4个 | C、3个 | D、2个 |
在等差数列{an}中,a3+a5=10,a7=2,则a1=( )
| A、5 | B、8 | C、10 | D、14 |
过点A(1,2)且与原点距离最大的直线方程为( )
| A、2x+y-4=0 |
| B、x+2y-5=0 |
| C、x+3y-7=0 |
| D、3x+y-5=0 |
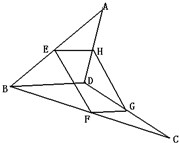 如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,求证:BD∥面EFGH.
如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,求证:BD∥面EFGH.