Question

如图，在Rt△ABC中，∠A=90°，D是AC上一点，E是BC上一点，若AB=

1

2

BD，CE=

1

2

EB，∠BDE=120°，CD=3，则BC=

 

．

Answer 1

考点：余弦定理

专题：解三角形

分析：经E点作EF⊥AC于F点，设AB=x，则由题意可求得BD，AD，AC，BC²，EF，ED，△EDB中，由余弦定理知：

4

9

x²+4x²-2×

2x

3

×4x²×（-

1

2

）=

4

9

BC²=

4

9

x²+(3+

3

x)2，整理可得：3x²-2

2

x-3=9，可解得x，从而可求BC．

解答：
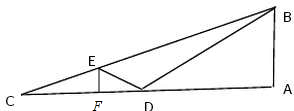
解：如图，经E点作EF⊥AC于F点，设AB=x，则由题意可得，
BD=2x，AD=

3

x，AC=3+

3

x，BC²=x²+(3+

3

x)2，
∵△CEF∽△ABC，∴

EF

AB

=

EC

BC

=

1

3

，即有EF=

1

3

x，
∵∠BDE=120°，AB=

1

2

BD，
∴∠EDF=30°，∴ED=2EF=

2

3

x，
∴△EDB中，由余弦定理知：BE²=DE²+BD²-2ED×BD×cos120°=

4

9

x²+4x²-2×

2x

3

×4x²×（-

1

2

）=

4

9

BC²
=

4

9

[x²+(3+

3

x)2]，
整理可得：3x²-2

2

x-3=9，
∴可解得：x=

3

或-

3

3

（舍去），
∴BC²=x²+(3+

3

x)2=39，可解得：BC=

39

．
故答案为：

39

．

点评：本题主要考察了余弦定理的应用，属于基本知识的考查．