题目内容
 (1)设x,y∈R,向量
(1)设x,y∈R,向量| a |
| b |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
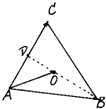
(2)设0为△ABC的外心,已知AB=3,AC=4,非零实数x,y满足
| AO |
| AB |
| AC |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:(1)根据向量的平行和垂直线求出x,y值,然后求解即可;
(2取去AC的中点,证明0、B、D共线,在Rt△ADB中求cos∠BAC的值.
(2取去AC的中点,证明0、B、D共线,在Rt△ADB中求cos∠BAC的值.
解答:
解:(1)∵
⊥
;
∴2x-4=0;x=2,
又
∥
;
∴-4-2y=0;y=-2
∴
=(2,1),
=(1,-2),
+
=(3,-1),|
+
|=
=
…(4分)
设
+
与
的夹角为θ,
则cosθ=
=
=
;
∵0≤θ≤π;
∴θ=
即
+
与
的夹角为
…(7分)
(2)设AC的中点为D
∵
=x
+y
=x
+2y
;
又x+2y=1;O、B、D三点共线…(12分)
由O为△ABC外心知OD⊥AC,BD⊥AC在Rt△ADB中,AB=3,AD=
AC=2
∴cos∠BAC=
=
…(14分)
| a |
| c |
∴2x-4=0;x=2,
又
| b |
| c |
∴-4-2y=0;y=-2
∴
| a |
| b |
| a |
| b |
| a |
| b |
| 32+(-1)2 |
| 10 |
设
| a |
| b |
| c |
则cosθ=
(
| ||||||
|
|
| 3×2+(-1)×(-4) | ||||
|
| ||
| 2 |
∵0≤θ≤π;
∴θ=
| π |
| 4 |
即
| a |
| b |
| c |
| π |
| 4 |
(2)设AC的中点为D
∵
| AO |
| AB |
| AC |
| AB |
| AD |
又x+2y=1;O、B、D三点共线…(12分)
由O为△ABC外心知OD⊥AC,BD⊥AC在Rt△ADB中,AB=3,AD=
| 1 |
| 2 |
∴cos∠BAC=
| AD |
| AB |
| 2 |
| 3 |
点评:本题主要考查向量的平行、垂直,夹角、模等知识点.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
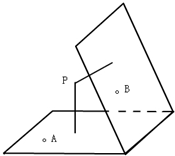 如图,P为60°的二面角α-l-β内一点,P到二面角两个面的距离分别为2、3,A、B是二面角的两个面内的动点,则△PAB周长的最小值为
如图,P为60°的二面角α-l-β内一点,P到二面角两个面的距离分别为2、3,A、B是二面角的两个面内的动点,则△PAB周长的最小值为