题目内容
已知中心在原点的椭圆C的右焦点为(
,0),右顶点为(2,0),
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=kx+
与椭圆C恒有两个不同的交点A和B,且
•
>2(其中O为原点),求k的取值范围.
| 3 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=kx+
| 2 |
| OA |
| OB |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:向量与圆锥曲线
分析:(Ⅰ)直接由题意得到a,c的值,利用隐含条件求得b的值,则椭圆方程可求;
(Ⅱ)联立直线和椭圆方程,化为关于x的一元二次方程后利用根与系数关系得到A,B两点横坐标的和与积,结合
•
>2求得k的范围,再由判别式大于0求得k的范围,取交集后得答案.
(Ⅱ)联立直线和椭圆方程,化为关于x的一元二次方程后利用根与系数关系得到A,B两点横坐标的和与积,结合
| OA |
| OB |
解答:
解:(Ⅰ)由题意可得:a=2,c=
,
∴b=
=
=1,
∴所求的椭圆方程为:
+y2=1;
(Ⅱ)设A(x1,y1),B(x2,y2),
由
得:(
+k2)x2+2
kx+1=0.
∴x1+x2=
,x1x2=
(*)
△=(2
k)2-4•(
+k2)>0,解得:k>
或k<-
.
由
•
>2,可得:x1x2+y1y2>2,即x1x2+(kx1+
)(kx2+
)>2.
整理得:(1+k2)x1x2+
k(x1+x2)>0.
把(*)代入得:(1+k2)•
+
k•
>0,即:
>0.
解得:-
<k<
.
综上:k的取值范围是-
<k<-
或
<k<
.
| 3 |
∴b=
| a2-c2 |
| 4-3 |
∴所求的椭圆方程为:
| x2 |
| 4 |
(Ⅱ)设A(x1,y1),B(x2,y2),
由
|
| 1 |
| 4 |
| 2 |
∴x1+x2=
-2
| ||
|
| 1 | ||
|
△=(2
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
由
| OA |
| OB |
| 2 |
| 2 |
整理得:(1+k2)x1x2+
| 2 |
把(*)代入得:(1+k2)•
| 1 | ||
|
| 2 |
(-2
| ||
|
| 4-12k2 |
| 1+4k2 |
解得:-
| ||
| 3 |
| ||
| 3 |
综上:k的取值范围是-
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
点评:本题考查了椭圆方程的求法,考查了直线与圆锥曲线的关系,涉及直线与圆锥曲线关系问题常采用联立直线方程和圆锥曲线方程,化为关于x的一元二次方程后利用根与系数的关系求解,特点是计算量较大,要求考生具有较强的运算能力,是压轴题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
集合M={x|(x+2)(x-2)≤0},N={x|-1<x<3},则M∩N=( )
| A、{x|-1≤x<2} |
| B、{x|-1<x≤2} |
| C、{x|-2≤x<3} |
| D、{x|-2<x≤2} |
设x,y满足约束条件
,则z=2x-y的最大值为( )
|
| A、10 | B、8 | C、3 | D、2 |

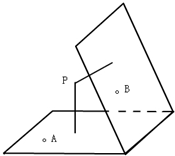 如图,P为60°的二面角α-l-β内一点,P到二面角两个面的距离分别为2、3,A、B是二面角的两个面内的动点,则△PAB周长的最小值为
如图,P为60°的二面角α-l-β内一点,P到二面角两个面的距离分别为2、3,A、B是二面角的两个面内的动点,则△PAB周长的最小值为