题目内容
10.已知{an}是各项为正数的等差数列,Sn为其前n项和,且4Sn=(an+1)2.(Ⅰ)求a1,a2的值及{an}的通项公式;
(Ⅱ)求数列$\{{S_n}-\frac{7}{2}{a_n}\}$的最小值.
分析 (Ⅰ)由于4Sn=(an+1)2.令n=1,可求得a1,再令n=2,即可求得a2的值,从而可得正项等差数列{an}的公差,继而可求得其通项公式;
(Ⅱ)由(Ⅰ)知an=2n-1,于是可求得其前n项和Sn=n2,故${S}_{n}-\frac{7}{2}{a}_{n}$=${(n-\frac{7}{2})}^{2}-\frac{35}{4}$,从而可求得数列$\{{S_n}-\frac{7}{2}{a_n}\}$的最小值.
解答 (本小题满分13分)
解:(Ⅰ)因为$4{S_n}={({a_n}+1)^2}$,
所以,当n=1时,$4{a_1}={({a_1}+1)^2}$,解得a1=1,
当n=2时,$4(1+{a_2})={({a_2}+1)^2}$,解得a2=-1或a2=3,
因为{an}是各项为正数的等差数列,所以a2=3,
所以{an}的公差d=a2-a1=2,
所以{an}的通项公式an=a1+(n-1)d=2n-1.
(Ⅱ)因为$4{S_n}={({a_n}+1)^2}$,所以${S_n}=\frac{{{{(2n-1+1)}^2}}}{4}={n^2}$,
所以${S_n}-\frac{7}{2}{a_n}={n^2}-\frac{7}{2}(2n-1)$=${n^2}-7n+\frac{7}{2}$=${(n-\frac{7}{2})^2}-\frac{35}{4}$,
所以,当n=3或n=4时,${S_n}-\frac{7}{2}{a_n}$取得最小值$-\frac{17}{2}$.
点评 本题考查数列递推式的应用,考查等差数列的通项公式及二次函数的配方法求最值,属于中档题.

练习册系列答案
相关题目
20.设i为虚数单位,若复数$\frac{z}{-i}$在复平面内对应的点为(1,2),则z=( )
| A. | -2+i | B. | 2-i | C. | -1+2i | D. | 1-2i |
18.若集合A={-2,0,1},B={x|x<-1或x>0},则A∩B=( )
| A. | {-2} | B. | {1} | C. | {-2,1} | D. | {-2,0,1} |
2.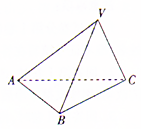 如图所示,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,若以垂直于平面VAC的方向作为正视图的方向,垂直于平面ABC的方向为俯视图的方向,已知其正视图的面积为2$\sqrt{3}$,则其侧视图的面积是( )
如图所示,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,若以垂直于平面VAC的方向作为正视图的方向,垂直于平面ABC的方向为俯视图的方向,已知其正视图的面积为2$\sqrt{3}$,则其侧视图的面积是( )
 如图所示,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,若以垂直于平面VAC的方向作为正视图的方向,垂直于平面ABC的方向为俯视图的方向,已知其正视图的面积为2$\sqrt{3}$,则其侧视图的面积是( )
如图所示,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,若以垂直于平面VAC的方向作为正视图的方向,垂直于平面ABC的方向为俯视图的方向,已知其正视图的面积为2$\sqrt{3}$,则其侧视图的面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3 |
19.某校为了解800名高一新生的身体生长状况,用系统抽样法(按等距的规则)抽取50名同学进行检查,将学生从1~800进行编号,现已知第17组抽取的号码为263,则第一组用简单随机抽样抽取的号码为7.
20.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点为F1、F2,其中一条渐近线方程为y=3x,过点F2作x轴的垂线与双曲线的一个交点为M,若△MF1F2的面积为18$\sqrt{10}$,则双曲线的方程为( )
| A. | x2-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{9}$-y2=1 | C. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{18}$=1 | D. | $\frac{{x}^{2}}{18}$-$\frac{{y}^{2}}{2}$=1 |
 如图,四边形ABCD为直角梯形,∠ABC=90°,CB∥DA,AB=20$\sqrt{2}$,DA=10,CB=20,若AB边上有一点P,使得∠CPD最大,则AP=10$\sqrt{2}$.
如图,四边形ABCD为直角梯形,∠ABC=90°,CB∥DA,AB=20$\sqrt{2}$,DA=10,CB=20,若AB边上有一点P,使得∠CPD最大,则AP=10$\sqrt{2}$.