题目内容
20.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点为F1、F2,其中一条渐近线方程为y=3x,过点F2作x轴的垂线与双曲线的一个交点为M,若△MF1F2的面积为18$\sqrt{10}$,则双曲线的方程为( )| A. | x2-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{9}$-y2=1 | C. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{18}$=1 | D. | $\frac{{x}^{2}}{18}$-$\frac{{y}^{2}}{2}$=1 |
分析 根据双曲线的渐近线方程,求得b=3a,求得M点坐标,根据三角形的面积公式,及双曲线的性质,即可求得a和b的值,即可求得双曲线方程.
解答 解:由双曲线的焦点在x轴上,双曲线的渐近线方程y=$\frac{b}{a}$x,则b=3a,①
假设M在第一象限,则M(c,$\frac{{b}^{2}}{a}$),
则△MF1F2的面积S=$\frac{1}{2}$×2c×$\frac{{b}^{2}}{a}$=$\frac{{b}^{2}c}{a}$,
即$\frac{{b}^{2}c}{a}$=18$\sqrt{10}$,②
则c2=a2-b2,③
解得:a2=2,b2=18,c2=20,
∴双曲线的标准方程:$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{18}=1$,
故选C.
点评 本题考查双曲线的标准方程及简单几何性质,三角形的面积公式,考查计算能力,属于中档题.

练习册系列答案
相关题目
8.已知变量x,y满足约束条件$\left\{\begin{array}{l}{y≤2}\\{x+y≥1}\\{x-y≤1}\end{array}\right.$,则z=3x+y的最小值为( )
| A. | -1 | B. | 1 | C. | 0 | D. | 11 |
9.若集合A={x|-1<x<2},B={x|-2<x<1},则集合A∪B=( )
| A. | {x|-1<x<1} | B. | {x|-2<x<1} | C. | {x|-2<x<2} | D. | {x|0<x<1} |
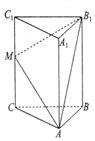 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8.
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8.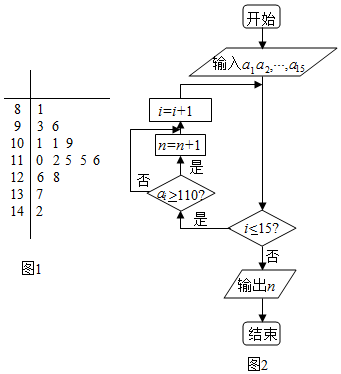 高三某班15名学生一次模拟考试成绩用茎叶图表示如图1,执行图2所示的程序框图,若输入的ai(i=1,2,…,15)分别为这15名学生的考试成绩,则输出的结果为( )
高三某班15名学生一次模拟考试成绩用茎叶图表示如图1,执行图2所示的程序框图,若输入的ai(i=1,2,…,15)分别为这15名学生的考试成绩,则输出的结果为( )