题目内容
1.三棱柱ABC-A1B1C1中,AA1与AC、AB所成角均为60°,∠BAC=90°,且AB=AC=AA1,则A1B与AC1所成角的正弦值为( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 连结A1C,交AC1于点E,取BC的中点D,连结AD、DE,则∠AED(或其补角)就是异面直线A1B与AC1所成的角,由此能求出异面直线A1B与AC1所成角的余弦值.
解答 解:连结A1C,交AC1于点E,取BC的中点D,连结AD、DE,
∵四边形AA1C1C是平行四边形,∴E是A1C的中点
∵D是BC的中点,∴DE是△A1BC的中位线,可得DE$\underset{∥}{=}$$\frac{1}{2}$A1B,
因此,∠AED(或其补角)就是异面直线A1B与AC1所成的角.
设AB=AC=AA1=2,
∵∠A1AB=60°,∴△A1AB是等边三角形,可得A1B=2,
得DE=$\frac{1}{2}$A1B=1.
同理,等边△A1AC中,中线AE=$\frac{\sqrt{3}}{2}$A1A=$\sqrt{3}$,
又∵∠BAC=90°,AB=AC=2,D为BC中点,
∴AD=$\frac{1}{2}$BC=$\frac{1}{2}$$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{2}$,
由此可得△ADE中,cos∠AED=$\frac{A{E}^{2}+D{E}^{2}-A{D}^{2}}{2AE•ED}$=$\frac{3+1-2}{2×\sqrt{3}×1}$=$\frac{\sqrt{3}}{3}$.
即异面直线A1B与AC1所成角的余弦值为$\frac{\sqrt{3}}{3}$.
故选:C.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
相关题目
6.函数y=$\frac{sinx}{|sinx|}$+$\frac{|cosx|}{cosx}$+$\frac{tanx}{|tanx|}$的值域是( )
| A. | {1} | B. | {1,3} | C. | {-1} | D. | {-1,3} |
13.下列命题中为真命题的是( )
| A. | 命题“若x>1,则x2>1”的否命题 | B. | 命题“若x>y,则x>|y|”的逆命题 | ||
| C. | 命题“若x=1,则x2+x-2=0”的否命题 | D. | 命题“若x2≥1,则x≥1”的逆否命题 |
 某飞机失联,经卫星侦查,其最后出现在小岛O附近.现派出四艘搜救船A,B,C,D,为方便联络,船A,B始终在以小岛O为圆心,100海里为半径的圆上,船A,B,C,D构成正方形编队展开搜索,小岛O在正方形编队外(如图).设小岛O到AB的距离为x,∠AOB=α,D船到小岛O的距离为d.
某飞机失联,经卫星侦查,其最后出现在小岛O附近.现派出四艘搜救船A,B,C,D,为方便联络,船A,B始终在以小岛O为圆心,100海里为半径的圆上,船A,B,C,D构成正方形编队展开搜索,小岛O在正方形编队外(如图).设小岛O到AB的距离为x,∠AOB=α,D船到小岛O的距离为d. 如图,在一个面积为8的矩形中随机撒一粒黄豆,若黄豆落到阴影部分的概率为$\frac{1}{4}$,则阴影部分的面积为2.
如图,在一个面积为8的矩形中随机撒一粒黄豆,若黄豆落到阴影部分的概率为$\frac{1}{4}$,则阴影部分的面积为2.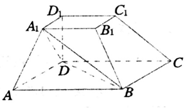 如图所示,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.
如图所示,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.