题目内容
6.函数y=$\frac{sinx}{|sinx|}$+$\frac{|cosx|}{cosx}$+$\frac{tanx}{|tanx|}$的值域是( )| A. | {1} | B. | {1,3} | C. | {-1} | D. | {-1,3} |
分析 由已知可得分母不为0,x终边不在坐标轴上,分类讨论,确定各个象限三角函数的符号,即可得解其值域.
解答 解:分母不为0,所以x终边不在坐标轴上,
若x在第一象限,
sinx>0,cosx>0,tanx>0,
可得:y=1+1+1=3,
若x在第二象限,
可得:sinx>0,cosx<0,tanx<0,
所以y=1-1-1=-1,
若x第三象限,
可得:y=-1-1+1=-1,
若x第四象限,
可得:y=-1+1-1=-1,
故值域为:{-1,3}.
故选:D.
点评 本题值域考查了三角函数求值,对角所在的象限讨论,确定三角函数的符号是解题的关键,属于基础题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
15.如图,网格纸上小正方形的边长为1,粗实线画出的某多面体的三视图,则该多面体的体积为( )

| A. | 8 | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
1.三棱柱ABC-A1B1C1中,AA1与AC、AB所成角均为60°,∠BAC=90°,且AB=AC=AA1,则A1B与AC1所成角的正弦值为( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
11.已知直线m、n与平面α,β,m⊥α,n⊥β,若α⊥β,则m、n的位置关系是( )
| A. | 平行 | B. | 垂直 | C. | 相交 | D. | 异面 |
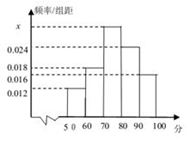 某校为了解高三开学数学考试的情 况,从高三的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60 )的学生人数为6.试根据样本估计“该校高三学生期末数学考试成绩≥70”的 概率为( )
某校为了解高三开学数学考试的情 况,从高三的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60 )的学生人数为6.试根据样本估计“该校高三学生期末数学考试成绩≥70”的 概率为( )