题目内容
已知函数f(x)=xlnx-x2+2mx+m,(m∈R).
(1)当m=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当x≥1时,若关于x的不等式f(x)≤0恒成立,试求m的取值范围.
(1)当m=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当x≥1时,若关于x的不等式f(x)≤0恒成立,试求m的取值范围.
考点:利用导数研究曲线上某点切线方程,函数恒成立问题,利用导数求闭区间上函数的最值
专题:计算题,导数的综合应用
分析:(1)求出导数,求出斜率和切点,由点斜式方程,即可得到切线方程;
(2)运用分离参数,得到x≥1,f(x)≤0⇒m≤
,设g(x)=
,求出g(x)的最小值,注意两次运用导数,即可得到最小值.
(2)运用分离参数,得到x≥1,f(x)≤0⇒m≤
| x2-xlnx |
| 2x+1 |
| x2-xlnx |
| 2x+1 |
解答:
解:(1)当m=1时,f(x)=xlnx-x2+2x+1,
f(1)=2,f′(1)=1,f′(x)=lnx-2x+3,
切线方程为y-2=x-1,
∴曲线y=f(x)在点(1,f(1))处的切线方程为:y=x+1;
(2)∵x≥1,f(x)≤0⇒m≤
,设g(x)=
,g′(x)=
=
,
设φ(x)=2x2-lnx-1,φ′(x)=4x-
=
∵x≥1,∴φ′(x)>0,则φ(x)在区间[1,+∞)上是单调递增函数,
∴x≥1时,φ(x)≥φ(1)=1>0,∴x≥1时,g′(x)>0,
则g(x)在区间[1,+∞)上是单调递增函数,
则g(x)在区间[1,+∞)上的最小值为g(1)=
,
当x≥1时,不等式f(x)≤0恒成立,则m≤
.
f(1)=2,f′(1)=1,f′(x)=lnx-2x+3,
切线方程为y-2=x-1,
∴曲线y=f(x)在点(1,f(1))处的切线方程为:y=x+1;
(2)∵x≥1,f(x)≤0⇒m≤
| x2-xlnx |
| 2x+1 |
| x2-xlnx |
| 2x+1 |
| (2x-lnx-1)(2x+1)-2(x2-xlnx) |
| (2x+1)2 |
| 2x2-lnx-1 |
| (2x+1)2 |
设φ(x)=2x2-lnx-1,φ′(x)=4x-
| 1 |
| x |
| 4x2-1 |
| x |
∵x≥1,∴φ′(x)>0,则φ(x)在区间[1,+∞)上是单调递增函数,
∴x≥1时,φ(x)≥φ(1)=1>0,∴x≥1时,g′(x)>0,
则g(x)在区间[1,+∞)上是单调递增函数,
则g(x)在区间[1,+∞)上的最小值为g(1)=
| 1 |
| 3 |
当x≥1时,不等式f(x)≤0恒成立,则m≤
| 1 |
| 3 |
点评:本题考查导数的运用:求切线方程,求单调区间和极值、最值,同时考查不等式恒成立问题转化为求函数的最值问题,注意运用导数,求单调区间和极值、最值,属于中档题.

练习册系列答案
相关题目
下列命题正确的有( )
①(1-
)8的展开式中所有项的系数和为0;
②命题p:“?x∈R,x02-x0-1>1”的否定¬p:“?x∈R,x2-x-1≤0”;
③设随机变量X服从正态分布N(0,1),若P(X>1)=p,P(-1<X<0)=
-p;
④回归直线一定过样本点的中心(
,
).
①(1-
| x |
②命题p:“?x∈R,x02-x0-1>1”的否定¬p:“?x∈R,x2-x-1≤0”;
③设随机变量X服从正态分布N(0,1),若P(X>1)=p,P(-1<X<0)=
| 1 |
| 2 |
④回归直线一定过样本点的中心(
. |
| x |
| y |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知
(
+
)=2,则a=( )
| lim |
| x→∞ |
| 2 |
| x-1 |
| ax-1 |
| x-1 |
| A、-6 | B、2 | C、3 | D、6 |
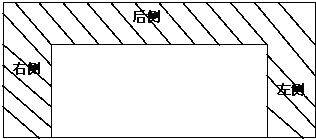 某村计划建造一个室内面积为72m2的矩形蔬菜温室.在温室内沿左、右两侧与后侧内墙各保留1m宽的通道,当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?
某村计划建造一个室内面积为72m2的矩形蔬菜温室.在温室内沿左、右两侧与后侧内墙各保留1m宽的通道,当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?