题目内容
袋中有4个黑球,3个白球,2个红球,从中任取2个球,每取到一个黑球得0分,每取到一个白球得1分,每取到一个红球得2分,用ξ表示分数,求ξ的概率分布.
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:由题意知ξ=0,1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列.
解答:
解:由题意知ξ=0,1,2,3,4,
P(ξ=0)=
=
=
,
P(ξ=1)=
=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
=
,
P(ξ=4)=
=
,
∴ξ的分布列为:
P(ξ=0)=
| ||
|
| 6 |
| 36 |
| 1 |
| 6 |
P(ξ=1)=
| ||||
|
| 12 |
| 36 |
| 1 |
| 3 |
P(ξ=2)=
| ||||||
|
| 11 |
| 36 |
P(ξ=3)=
| ||||
|
| 6 |
| 36 |
| 1 |
| 6 |
P(ξ=4)=
| ||
|
| 1 |
| 36 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
点评:本题考查离散型随机变量的分布列的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果(1-2x)9的展开式中第三项等于288,则
(
+
+…+
)等于( )
| lim |
| n→∞ |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| xn |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
阅读如图所示的程序框图,执行相应的程序,则输出的S值为( )


| A、31 | B、32 | C、63 | D、64 |
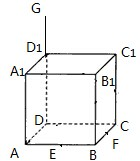 如图,G是正方体ABCD-A1B1C1D1的棱的DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出:
如图,G是正方体ABCD-A1B1C1D1的棱的DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出: