题目内容
已知函数f(x)=x2+2x,
(1)若f(x)在[a,+∞)上是增函数,求a的取值范围.
(2)当x∈[2,5]时,求f(x)的最值.
(1)若f(x)在[a,+∞)上是增函数,求a的取值范围.
(2)当x∈[2,5]时,求f(x)的最值.
考点:二次函数在闭区间上的最值,二次函数的性质
专题:函数的性质及应用
分析:(1)由于函数f(x)=x2+2x在[a,+∞)上是增函数,可得a≥-1,即为所求的a的范围.
(2)当x∈[2,5]时,f(x)=x2+2x=(x+1)2-1是增函数,从而求得函数f(x)的最值.
(2)当x∈[2,5]时,f(x)=x2+2x=(x+1)2-1是增函数,从而求得函数f(x)的最值.
解答:
解:(1)∵函数f(x)=x2+2x在[a,+∞)上是增函数,∴a≥-1,即a的范围是[-1,+∞).
(2)当x∈[2,5]时,f(x)=x2+2x=(x+1)2-1是增函数,故当x=2时,函数取得最小值为8,当x=5时,函数取得最大值为35.
(2)当x∈[2,5]时,f(x)=x2+2x=(x+1)2-1是增函数,故当x=2时,函数取得最小值为8,当x=5时,函数取得最大值为35.
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了转化的数学思想,属基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
若点O和点F分别为椭圆
+y2=1的中心和右焦点,点P为椭圆上的任意一点,则
•
的最小值为( )
| x2 |
| 2 |
| OP |
| FP |
A、2-
| ||
B、
| ||
C、2+
| ||
| D、1 |
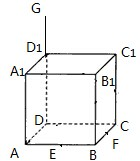 如图,G是正方体ABCD-A1B1C1D1的棱的DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出:
如图,G是正方体ABCD-A1B1C1D1的棱的DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出: