题目内容
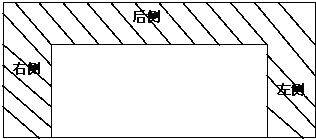某村计划建造一个室内面积为72m2的矩形蔬菜温室．在温室内沿左、右两侧与后侧内墙各保留1m宽的通道，当矩形温室的边长各为多少时？蔬菜的种植面积最大，最大种植面积是多少？考点：基本不等式在最值问题中的应用
专题：应用题,不等式的解法及应用
分析：设出温室的长为xm，建立蔬菜面积关于矩形边长的函数关系S（x）=（x-2）（
-1），然后利用基本不等式研究函数的最值．
| 72 |
| x |
解答：
解：设温室的长为xm，则宽为
m（x＞0）
则可种植蔬菜的面积S（x）=（x-2）（
-1）=74-（x+
）
∵x+
≥24，∴S（x）≤50
∴在x=12时，g（x）取得最小值，S（x）取得最大值50m2．
答：温室的长为40m时，蔬菜的种植面积最大为50m2．
| 72 |
| x |
则可种植蔬菜的面积S（x）=（x-2）（
| 72 |
| x |
| 144 |
| x |
∵x+
| 144 |
| x |
∴在x=12时，g（x）取得最小值，S（x）取得最大值50m2．
答：温室的长为40m时，蔬菜的种植面积最大为50m2．
点评：本题主要考查了函数的最值的应用题，同理考查了利用基本不等式研究函数的最值，属于中档题．
练习册系列答案
相关题目
集合M中的元素都是正整数，且若a∈M，则6-a∈M，则所有满足条件的集合M共有（ ）
| A、6个 | B、7个 | C、8个 | D、9个 |
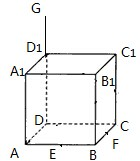如图，G是正方体ABCD-A1B1C1D1的棱的DD1延长线上的一点，E、F是棱AB、BC的中点，试分别画出：