题目内容
函数f(x)=log2
•log
(2x)的最小值为 .
| x |
| 2 |
考点:对数的运算性质
专题:函数的性质及应用
分析:利用对数的运算性质进行化简转化为一元二次函数求最值即可.
解答:
解:因为函数f(x)=log2
•log
(2x),所以函数的定义域为{x|x>0},
又f(x)=log2
•log
(2x)
=(log2x)2+log2x=(log2x+
)2-
所以,当log2x=-
,即x=
时,f(x)取得最小值-
,
故答案为:-
.
| x |
| 2 |
又f(x)=log2
| x |
| 2 |
=(log2x)2+log2x=(log2x+
| 1 |
| 2 |
| 1 |
| 4 |
所以,当log2x=-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
故答案为:-
| 1 |
| 4 |
点评:本题主要考查对数的运算性质和一元二次函数的最值.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
集合M中的元素都是正整数,且若a∈M,则6-a∈M,则所有满足条件的集合M共有( )
| A、6个 | B、7个 | C、8个 | D、9个 |
对给出的下列命题:
①?x∈R,-x2<0;
②?x∈Q,x2=5;
③?x∈R,x2-x-1=0;
④若p:?x∈N,x2≥1,则¬p:?x∈N,x2<1.
其中是真命题的是( )
①?x∈R,-x2<0;
②?x∈Q,x2=5;
③?x∈R,x2-x-1=0;
④若p:?x∈N,x2≥1,则¬p:?x∈N,x2<1.
其中是真命题的是( )
| A、①③ | B、②④ | C、②③ | D、③④ |
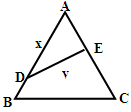 如图,公园有一块边长为2的等边的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.设AD=x(x≥0),DE=y,求用x表示y的函数关系式,并求函数的定义域.
如图,公园有一块边长为2的等边的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.设AD=x(x≥0),DE=y,求用x表示y的函数关系式,并求函数的定义域.