题目内容
求数列
,
,
,
…的前n项和Sn.
| 22 |
| 22-1 |
| 42 |
| 42-1 |
| 62 |
| 62-1 |
| 82 |
| 82-1 |
考点:数列的求和
专题:等差数列与等比数列
分析:Sn═(1+
)+(1+
)+(1+
)+…+(1+
)=n+
×[(1-
)+(
-
)+(
-
)+…+(
-
)],由此能求出结果.
| 1 |
| 22-1 |
| 1 |
| 42-1 |
| 1 |
| 62-1 |
| 1 |
| (2n)2-1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
解:Sn=
+
+
+
=(1+
)+(1+
)+(1+
)+…+(1+
)
=n+
×[
×(2+1)+
×(4+1)+
×(6+1)+…+
×(2n+1)]
=n+
×[(3-1)×3+
×5+
×7+…+
×(2n+1)]
=n+
×[(1-
)+(
-
)+(
-
)+…+(
-
)]
=n+
×(1-
)
=n+
.
| 22 |
| 22-1 |
| 42 |
| 42-1 |
| 62 |
| 62-1 |
| (2n)2 |
| (2n)2-1 |
=(1+
| 1 |
| 22-1 |
| 1 |
| 42-1 |
| 1 |
| 62-1 |
| 1 |
| (2n)2-1 |
=n+
| 1 |
| 2 |
| 2 |
| 2-1 |
| 2 |
| 4-1 |
| 2 |
| 6-1 |
| 2 |
| 2n-1 |
=n+
| 1 |
| 2 |
| 5-3 |
| 3 |
| 7-5 |
| 5 |
| (2n+1)-(2n-1) |
| 2n-1 |
=n+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=n+
| 1 |
| 2 |
| 1 |
| 2n+1 |
=n+
| n |
| 2n+1 |
点评:本题考查数列前n项和的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知曲线y=x3+ax+b与斜率为2的直线相切于点A(1,3),则b的值为( )
| A、3 | B、-3 | C、5 | D、-5 |
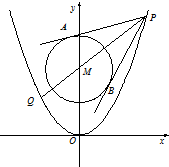 已知抛物线C1:x2=2py(p>0),圆C2:x2+y2-8y+12=0的圆心M到抛物线C1的准线的距离为
已知抛物线C1:x2=2py(p>0),圆C2:x2+y2-8y+12=0的圆心M到抛物线C1的准线的距离为