题目内容
从集合{1,2,3,4,5}中每次不放回地抽取一个数,直到奇数、偶数两类数中有一类全部抽完为止,
(1)求事件“抽了两次后还未停止”的概率;
(2)记X表示停止抽数时已从集合中抽出的数的个数,求X的分布列和期望.
(1)求事件“抽了两次后还未停止”的概率;
(2)记X表示停止抽数时已从集合中抽出的数的个数,求X的分布列和期望.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(1)利用对立事件的概率公式能求出事件“抽了两次后还未停止的概率.
(2)由题意知X=2,3,4,分别求出相应的概率,由此能求出X的分布列和EX.
(2)由题意知X=2,3,4,分别求出相应的概率,由此能求出X的分布列和EX.
解答:
解:(1)设事件A表示“抽了两次后还未停止”,
则
表示“抽了两次后停止”.
P(A)=1-P(
)=1-
×
=
.
(2)由题意知X=2,3,4,
P(X=2)=
×
=
,
P(X=3)=
×
×
+
×
×
+
×
×
=
,
P(X=4)=1-
-
=
,
∴X的分布列为:
∴EX=2×
+3×
+4×
=3.5.
则
. |
| A |
P(A)=1-P(
. |
| A |
| 2 |
| 5 |
| 1 |
| 4 |
| 9 |
| 10 |
(2)由题意知X=2,3,4,
P(X=2)=
| 2 |
| 5 |
| 1 |
| 4 |
| 1 |
| 10 |
P(X=3)=
| 3 |
| 5 |
| 2 |
| 4 |
| 1 |
| 3 |
| 3 |
| 5 |
| 2 |
| 4 |
| 1 |
| 3 |
| 2 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 3 |
| 10 |
P(X=4)=1-
| 1 |
| 10 |
| 3 |
| 10 |
| 3 |
| 5 |
∴X的分布列为:
| X | 2 | 3 | 4 | ||||||
| P |
|
|
|
| 1 |
| 10 |
| 3 |
| 10 |
| 3 |
| 5 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
相关题目
已知角α的始边为x轴正半轴,终边上有一点P(m,n)(n≠0)若α=-420°,则
的值为( )
| n |
| m |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
正数x,y,z满足:5z-3x≤y≤4z-x,z•lny≥x+z•lnz,则
的最大值为( )
| y |
| x |
| A、7 | B、8 | C、9 | D、10 |
a>b>1,P=
,Q=
(lga+lgb),R=
,则( )
| lga•lgb |
| 1 |
| 2 |
| a+b |
| 2 |
| A、.R<P<Q |
| B、.P<Q<R |
| C、Q<P<R |
| D、.P<R<Q |
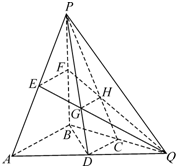 如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连结GH.
如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连结GH.