题目内容
p:函数f(x)=lg(x2+mx+1)的值域是Rq:x2-2mx+2m+3≤0的解集是∅,若p∧q为假,p∨q为真.求实数m的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:先求出命题p,q下的m的取值,由p∧q为假,p∨q为真知p,q中一真一假,所以分成p真q假,和p假q真两种情况求m的取值,再求并集即可.
解答:
解:∵p∧q为假,p∨q为真;
∴p,q一真一假;
要使p:函数f(x)=lg(x2+mx+1)的值域是R,必须:△=m2-4≥0,即m≥2,或m≤-2;
要使q:x2-2mx+2m+3≤0的解集是∅,必须:△=4m2-4(2m+3)<0即,-1<m<3;
当p真q假时
,解得m≥3,或m≤-2;
当p假q真时
,解得-1<m<2;
综上可知,m的取值范围是:(-∞,-2]∪(-1,2)∪[3,+∞).
∴p,q一真一假;
要使p:函数f(x)=lg(x2+mx+1)的值域是R,必须:△=m2-4≥0,即m≥2,或m≤-2;
要使q:x2-2mx+2m+3≤0的解集是∅,必须:△=4m2-4(2m+3)<0即,-1<m<3;
当p真q假时
|
当p假q真时
|
综上可知,m的取值范围是:(-∞,-2]∪(-1,2)∪[3,+∞).
点评:考查对数函数的值域,定义域,二次函数取值和判别式△的关系,一元二次不等式的解和判别式△的关系,p∧q,p∨q真假情况.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
设以
=(1,-2)为方向向量的直线的倾斜角为α,则sin(2α+
)=( )
. |
| e |
| π |
| 4 |
A、
| ||||
B、7
| ||||
C、
| ||||
D、-
|
已知函数f(x)=ln(1+x)-
,若x≥0时,f(x)≤0,则λ的最小值为( )
| x(1+λx) |
| 1+x |
| A、0 | ||
B、
| ||
| C、1 | ||
| D、2 |
设F1,F2是双曲线
-
=1的焦点,P是双曲线上一点.若P到F1的距离为9,则P到F2的距离等于( )
| x2 |
| 16 |
| y2 |
| 20 |
| A、0 | ||
| B、17 | ||
C、
| ||
| D、2 |
已知幂函数y=f(x)的图象经过点(8,
),则f(
)的值为( )
| 1 |
| 2 |
| 1 |
| 64 |
| A、3 | ||
B、
| ||
| C、4 | ||
D、
|
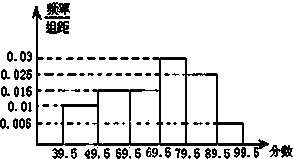 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题: