题目内容
正数x,y,z满足:5z-3x≤y≤4z-x,z•lny≥x+z•lnz,则
的最大值为( )
| y |
| x |
| A、7 | B、8 | C、9 | D、10 |
考点:简单线性规划
专题:不等式的解法及应用
分析:通过变形化简已知条件为
,
的不等式,利用表达式的几何意义,求解即可.
| x |
| z |
| y |
| z |
解答:
 解:5z-3x≤y≤4z-x,化为:5-
解:5z-3x≤y≤4z-x,化为:5-
≤
≤4-
.
z•lny≥x+z•lnz,化为:
≥e
,
令X=
,Y=
,
不等式化为:
=
=
.
画出
的可行域如图阴影部分:
的几何意义是可行域内的点与原点连线的斜率,由图象可知OA连线的斜率最大,由
可得A(
,
),
的最大值为
的最大值:7.
故选:A.
 解:5z-3x≤y≤4z-x,化为:5-
解:5z-3x≤y≤4z-x,化为:5-| 3x |
| z |
| y |
| z |
| x |
| z |
z•lny≥x+z•lnz,化为:
| y |
| z |
| x |
| z |
令X=
| x |
| z |
| y |
| z |
不等式化为:
|
| y |
| x |
| ||
|
| Y |
| X |
画出
|
| Y |
| X |
|
| 1 |
| 2 |
| 7 |
| 2 |
| y |
| x |
| Y |
| X |
故选:A.
点评:本题考查线性规划的应用,考查转化思想以及计算能力,转化不等式组为
是解题的关键.
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若a=log2π,b=log2
,c=log3
,则a,b,c的大小关系是( )
| 3 |
| 2 |
| A、b>a>c |
| B、b>c>a |
| C、a>b>c |
| D、a>c>b |
如果椭圆有两个顶点为(3,0),(0,-4),则其标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=
若|f(x)|≥a(x-1),则a的取值范围是( )
|
| A、(-∞,-1) |
| B、[-1,1] |
| C、[0,1] |
| D、[-1,0] |
 在某次测量中,在A处测得同一方向的B点的仰角为60°,C点的俯角为70°,则∠BAC等于( )
在某次测量中,在A处测得同一方向的B点的仰角为60°,C点的俯角为70°,则∠BAC等于( )| A、10° | B、50° |
| C、120° | D、130° |
已知函数f(x)=ln(1+x)-
,若x≥0时,f(x)≤0,则λ的最小值为( )
| x(1+λx) |
| 1+x |
| A、0 | ||
B、
| ||
| C、1 | ||
| D、2 |
执行图的程序框图,若输入的a,b,k分别为1,2,3,则输出的M=( )


A、
| ||
B、
| ||
C、
| ||
D、
|
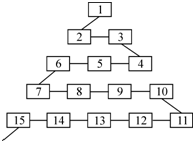 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…;依此类推,则
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…;依此类推,则