题目内容
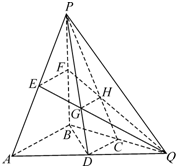 如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连结GH.
如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连结GH.(Ⅰ)求证:AB∥GH;
(Ⅱ)求平面PAB与平面PCD所成角的正弦值.
考点:二面角的平面角及求法,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知得EF∥AB,DC∥AB,从而EF∥DC.进而EF∥平面PCD. 由此能证明AB∥GH.
(Ⅱ)以B为坐标原点,分别以BA,BQ,BP所在直线为x轴,y轴,z轴,建立空间直角坐标系.利用向量法能求出平面PAB与平面PCD所成角的正弦值.
(Ⅱ)以B为坐标原点,分别以BA,BQ,BP所在直线为x轴,y轴,z轴,建立空间直角坐标系.利用向量法能求出平面PAB与平面PCD所成角的正弦值.
解答:
 (本小题满分12分)
(本小题满分12分)
(Ⅰ)证明:∵D,C,E,F分别是AQ,BQ,AP,BP的中点,…(1分)
∴EF∥AB,DC∥AB,…(2分)
∴EF∥DC.
又EF?平面PCD,DC?平面PCD,
∴EF∥平面PCD. …(3分)
又EF?平面EFQ,平面EFQ∩平面PCD=GH,…(4分)
∴EF∥GH.
又EF∥AB,
∴AB∥GH.…(6分)
(Ⅱ)解:在△ABQ中,∵AQ=2BD,AD=DQ,∴∠ABQ=90°,即AB⊥BQ.
又PB⊥平面ABQ,∴BA,BQ,BP两两垂直.
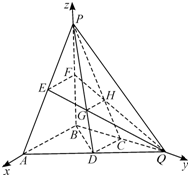
以B为坐标原点,分别以BA,BQ,BP所在直线为x轴,y轴,z轴,
建立如图所示的空间直角坐标系.设BA=BQ=BP=2,
则B(0,0,0),Q(0,2,0),D(1,1,0),
C(0,1,0),P(0,0,2),
∴
=(-1,-1,2),
=(0,-1,2).…(8分)
设平面PCD的一个法向量为
=(x,y,z),
由
•
=0,
•
=0,得
,取z=1,得
=(0,2,1).…(10分)
又
=(0,2,0)为平面PAB的一个法向量,
∴cos<n,
>=
=
.
设平面PAB与平面PCD所成角为θ,
则sinθ=
=
.
故平面PAB与平面PCD所成角的正弦值为
.…(12分)
 (本小题满分12分)
(本小题满分12分)(Ⅰ)证明:∵D,C,E,F分别是AQ,BQ,AP,BP的中点,…(1分)
∴EF∥AB,DC∥AB,…(2分)
∴EF∥DC.
又EF?平面PCD,DC?平面PCD,
∴EF∥平面PCD. …(3分)
又EF?平面EFQ,平面EFQ∩平面PCD=GH,…(4分)
∴EF∥GH.
又EF∥AB,
∴AB∥GH.…(6分)
(Ⅱ)解:在△ABQ中,∵AQ=2BD,AD=DQ,∴∠ABQ=90°,即AB⊥BQ.
又PB⊥平面ABQ,∴BA,BQ,BP两两垂直.
以B为坐标原点,分别以BA,BQ,BP所在直线为x轴,y轴,z轴,
建立如图所示的空间直角坐标系.设BA=BQ=BP=2,
则B(0,0,0),Q(0,2,0),D(1,1,0),
C(0,1,0),P(0,0,2),
∴
| DP |
| CP |
设平面PCD的一个法向量为
| n |
由
| n |
| DP |
| n |
| CP |
|
| n |
又
| BQ |
∴cos<n,
| BQ |
| 2×2 | ||
|
2
| ||
| 5 |
设平面PAB与平面PCD所成角为θ,
则sinθ=
1-(
|
| ||
| 5 |
故平面PAB与平面PCD所成角的正弦值为
| ||
| 5 |
点评:本题考查两条直线平行的证明,考查平面与平面所成角的正弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果椭圆有两个顶点为(3,0),(0,-4),则其标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
执行图的程序框图,若输入的a,b,k分别为1,2,3,则输出的M=( )


A、
| ||
B、
| ||
C、
| ||
D、
|
下列集合中为空集的是( )
| A、{x∈N|x2≤0} |
| B、{x∈R|x2-1=0} |
| C、{x∈R|x2+x+1=0} |
| D、{0} |
 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题: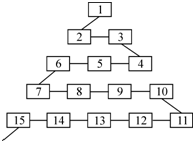 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…;依此类推,则
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…;依此类推,则