题目内容
点(
,2)在幂函数f(x)的图象上,点(-2,
)在幂函数g(x)的图象上.
(1)求f(x)与g(x)的解析式;
(2)当x为何值时,有f(x)>g(x).
| 2 |
| 1 |
| 4 |
(1)求f(x)与g(x)的解析式;
(2)当x为何值时,有f(x)>g(x).
考点:幂函数的单调性、奇偶性及其应用
专题:函数的性质及应用
分析:(1)根据幂函数的定义,利用待定系数法即可求f(x)与g(x)的解析式;
(2)根据幂函数的性质即可解不等式.
(2)根据幂函数的性质即可解不等式.
解答:
 解:(1)设f(x)=xα,则由题意得2=(
解:(1)设f(x)=xα,则由题意得2=(
)α,
∴α=2,即f(x)=x2,
再设g(x)=xβ,则由题意得
=(-2)β,β=-2,
即g(x)=x-2.
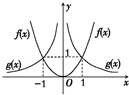
(2)在同一坐标系中作出f(x)与g(x)的图象,
如图所示.f(x)与g(x)交于(-1,1)点和(1,1)点,
由图象可知:当x>1或x<-1时,f(x)>g(x).
 解:(1)设f(x)=xα,则由题意得2=(
解:(1)设f(x)=xα,则由题意得2=(| 2 |
∴α=2,即f(x)=x2,
再设g(x)=xβ,则由题意得
| 1 |
| 4 |
即g(x)=x-2.
(2)在同一坐标系中作出f(x)与g(x)的图象,
如图所示.f(x)与g(x)交于(-1,1)点和(1,1)点,
由图象可知:当x>1或x<-1时,f(x)>g(x).
点评:本题主要考查幂函数的图象和性质的应用,利用待定系数法求出函数的解析式是解决本题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
已知点A(x,1,2)和点B(2,3,4),且|AB|=2
,则实数x的值是( )
| 6 |
| A、-3或4 | B、3或-4 |
| C、6或-2 | D、6或2 |
下列函数中,在其定义域上是增函数的是( )
| A、y=-2x | ||
B、y=(
| ||
C、y=log
| ||
D、y=x
|
某人射击一次命中目标的概率为
,则此人射击7次,3次命中且恰有2次连续命中的概率为( )
| 1 |
| 2 |
A、C
| |||||||
B、A
| |||||||
C、C
| |||||||
D、A
|