题目内容
对于数列{an},如果存在一个正整数T,使得对任意的n(n∈N*)都有an+T=an成立,那么数列{an}称作周期为T的周期数列,T的最小值称作数列{an}的最小正周期,以下简称周期.
(1)已知数列{an}的通项公式是an=cos
,判断数列{an}是否是周期数列?并说明理由;
(2)设数列{an}满足an+2=λ•an+1-an(n∈N*),a1=1,a2=2,且数列{an}是周期为3的周期数列,求常数λ的值;
(3)设数列{an}满足a1=1,a2=a(其中a是常数),an+an+1+an+2=cos
(n∈N*),求数列{an}的前2014项和S2014.
(1)已知数列{an}的通项公式是an=cos
| 2nπ |
| 3 |
(2)设数列{an}满足an+2=λ•an+1-an(n∈N*),a1=1,a2=2,且数列{an}是周期为3的周期数列,求常数λ的值;
(3)设数列{an}满足a1=1,a2=a(其中a是常数),an+an+1+an+2=cos
| 2nπ |
| 3 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由于an+3=an,即可得出.
(2)由数列{an}满足an+2=λ•an+1-an(n∈N*),a1=1,a2=2,可得a3,a4.利用数列{an}是周期为3的周期数列,可得1=2λ2-λ-2.解得λ即可..
(3)由于数列{an}满足a1=1,a2=a(其中a是常数),an+an+1+an+2=cos
(n∈N*),可得a2+a3+a4=…=a2012+a2013+a2014=cos
=-
.即可得出.
(2)由数列{an}满足an+2=λ•an+1-an(n∈N*),a1=1,a2=2,可得a3,a4.利用数列{an}是周期为3的周期数列,可得1=2λ2-λ-2.解得λ即可..
(3)由于数列{an}满足a1=1,a2=a(其中a是常数),an+an+1+an+2=cos
| 2nπ |
| 3 |
| 4π |
| 3 |
| 1 |
| 2 |
解答:
解:(1)∵an+3=cos
=cos(2π+
)=cos
=an,
∴数列{an}是周期为3的数列.
(2)∵数列{an}满足an+2=λ•an+1-an(n∈N*),a1=1,a2=2,
∴a3=2λ-1,a4=2λ2-λ-2.
∵数列{an}是周期为3的周期数列,∴1=2λ2-λ-2.解得λ=-1或
.经检验λ=-1.
(3)∵数列{an}满足a1=1,a2=a(其中a是常数),an+an+1+an+2=cos
(n∈N*),
∴a2+a3+a4=…=a2012+a2013+a2014=cos
=-
.
∴S2014=1+671(a2+a3+a4)=1-
=-
.
| 2(n+3)π |
| 3 |
| 2nπ |
| 3 |
| 2nπ |
| 3 |
∴数列{an}是周期为3的数列.
(2)∵数列{an}满足an+2=λ•an+1-an(n∈N*),a1=1,a2=2,
∴a3=2λ-1,a4=2λ2-λ-2.
∵数列{an}是周期为3的周期数列,∴1=2λ2-λ-2.解得λ=-1或
| 3 |
| 2 |
(3)∵数列{an}满足a1=1,a2=a(其中a是常数),an+an+1+an+2=cos
| 2nπ |
| 3 |
∴a2+a3+a4=…=a2012+a2013+a2014=cos
| 4π |
| 3 |
| 1 |
| 2 |
∴S2014=1+671(a2+a3+a4)=1-
| 671 |
| 2 |
| 669 |
| 2 |
点评:本题考查了数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
在2011年3月15日那天,南昌市物价部门对本市的5家商场的某商品的一天销售量及
由散点图可知,销售量y与价格x之间有较好的线性相关关系,根据上表可得回归直线方程是:
=-3.2x+a,则a=( )
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销量y | 11 | 10 | 8 | 6 | 5 |
 |
| y |
| A、-24 | B、35.6 |
| C、40.5 | D、40 |
下列函数中,增长速度最快的是( )
| A、y=5x |
| B、y=x5 |
| C、y=log5x |
| D、y=5x |
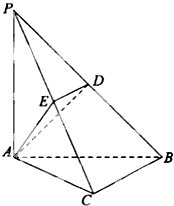 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱PB,PC上,且BC∥平面ADE.
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱PB,PC上,且BC∥平面ADE.
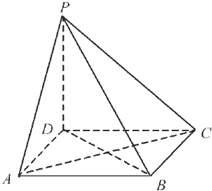 如图,在四棱锥P-ABCD中,底面ABCD是正方形,边长AB=a且PD=a,PA=PC=
如图,在四棱锥P-ABCD中,底面ABCD是正方形,边长AB=a且PD=a,PA=PC=