题目内容
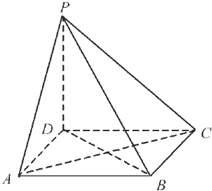 如图,在四棱锥P-ABCD中,底面ABCD是正方形,边长AB=a且PD=a,PA=PC=
如图,在四棱锥P-ABCD中,底面ABCD是正方形,边长AB=a且PD=a,PA=PC=| 2 |
考点:球的体积和表面积
专题:空间位置关系与距离
分析:设放入的球的半径为R,球心为S,当且仅当球与四棱锥的各个面都相切时,球的半径最大.连接SA、SB、SC、SD、SP,则把此四棱锥分割成四个三棱锥和一个四棱锥,这些小棱锥的高均为R,底面为原四棱锥的侧面或底面.由体积关系,得VP-ABCD=
(S△PAB+S△PBC+S△PCD+S△PAD+S正方形ABCD)即可得出.
| R |
| 3 |
解答:
解:设放入的球的半径为R,球心为S,当且仅当球与四棱锥的各个面都相切时,球的半径最大.
连接SA、SB、SC、SD、SP,则把此四棱锥分割成四个三棱锥和一个四棱锥,这些小棱锥的高均为R,底面为原四棱锥的侧面或底面.
由体积关系,得VP-ABCD=
(S△PAB+S△PBC+S△PCD+S△PAD+S正方形ABCD)
=
(
a2+
a2+
a2+
a2+a2)=
(2+
)a2,
∵VP-ABCD=
PD•S正方形ABCD=
a3,
∴
a3=
(2+
)a2,
解得R=
a.
∴球的最大半径是
a.
连接SA、SB、SC、SD、SP,则把此四棱锥分割成四个三棱锥和一个四棱锥,这些小棱锥的高均为R,底面为原四棱锥的侧面或底面.
由体积关系,得VP-ABCD=
| R |
| 3 |
=
| R |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| R |
| 3 |
| 2 |
∵VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
∴
| 1 |
| 3 |
| R |
| 3 |
| 2 |
解得R=
2-
| ||
| 2 |
∴球的最大半径是
2-
| ||
| 2 |
点评:本题考查了三棱锥的体积计算公式、求相切问题,考查了空间想象能力,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
若直线y=2x+b与曲线y=2-
有公共点,则b的取值范围是( )
| 4x-x2 |
A、[-2,2
| ||||
B、[-2
| ||||
C、[-2
| ||||
D、[2,2
|
从1,3,5,7,9这5个数中任取3个,这三个数能成为三角形三边的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若一直线过M(0,-1)且被圆(x-1)2+(y-2)2=25截得的弦AB长为8,则这条直线的方程是( )
| A、3x+4y+4=0 |
| B、3x+4y+4=0或y+1=0 |
| C、3x-4y-4=0 |
| D、3x-4y-4=0或y+1=0 |
若函数f(x)=2x-
+a在(2,+∞)是增函数,则a的取值范围是( )
| a |
| x |
| A、(-12,+∞) |
| B、[-12,+∞) |
| C、(-8,+∞) |
| D、[-8,+∞) |
a,b,c∈R,则下列命题正确的是( )
| A、若a2>b2,则a>b | ||||
| B、若a<b,则ac<bc | ||||
C、若a>b,则
| ||||
| D、若a>c,b>d,则a+b>c+d |
命题甲:sinx=a,命题乙:arcsina=x(-1≤a≤1),则( )
| A、甲是乙的充分条件,但不是必要条件 |
| B、甲是乙的必要条件,但不是充分条件 |
| C、甲是乙的充分必要条件 |
| D、甲不是乙的充分条件,也不是必要条件 |