题目内容
设函数f(x)=
,方程x=f(x)有唯一解,其中实数a为常数,f(x1)=
,f(xn)=xn+1(n∈N*).
(1)求f(x)的表达式;
(2)求x2015的值;
(3)若an=
-4023且bn=
(n∈N*),求证:b1+b2+…+bn<n+1.
| x |
| a(x+2) |
| 2 |
| 2013 |
(1)求f(x)的表达式;
(2)求x2015的值;
(3)若an=
| 4 |
| xn |
| ||||
| 2an+1an |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由x=
,得ax(x+2)=x(a≠0),由此能求出f(x)=
.
(2)由f(xn)=xn+1,得
=xn+1,从而数列{
}是以
为首项,
为公差的等差数列.由此能求出xn=
,从而x2015=
=
.
(3)由xn=
,得an=2n-1,从而bn=1+
-
,由此能证明b1+b2+…+bn<n+1.
| x |
| a(x+2) |
| 2x |
| x+2 |
(2)由f(xn)=xn+1,得
| 2xn |
| xn+2 |
| 1 |
| xn |
| 1 |
| x1 |
| 1 |
| 2 |
| 2 |
| n+2011 |
| 2 |
| 2015+2011 |
| 1 |
| 2013 |
(3)由xn=
| 2 |
| n+2011 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
(1)解:由x=
,得ax(x+2)=x(a≠0),
所以ax2+(2a-1)x=0,
当且仅当a=
时,方程x=f(x)有唯一解.
从而f(x)=
.
(2)解:由已知f(xn)=xn+1,得
=xn+1,
∴
=
+
,即
-
=
(n∈N*),
∴数列{
}是以
为首项,
为公差的等差数列.
∴
=
+(n-1)×
=
,故xn=
.
∵f(x1)=
,∴
=
,解得x1=
.
∴xn=
=
,故x2015=
=
.
(3)证明:∵xn=
,∴an=4×
-4 023=2n-1,
∴bn=
=
=
=1+
-
,
∴b1+b2+…+bn-n
=(1+1-
)+(1+
-
)+…+(1+
-
)-n
=1-
<1.
故b1+b2+…+bn<n+1.
| x |
| a(x+2) |
所以ax2+(2a-1)x=0,
当且仅当a=
| 1 |
| 2 |
从而f(x)=
| 2x |
| x+2 |
(2)解:由已知f(xn)=xn+1,得
| 2xn |
| xn+2 |
∴
| 1 |
| xn+1 |
| 1 |
| 2 |
| 1 |
| xn |
| 1 |
| xn+1 |
| 1 |
| xn |
| 1 |
| 2 |
∴数列{
| 1 |
| xn |
| 1 |
| x1 |
| 1 |
| 2 |
∴
| 1 |
| xn |
| 1 |
| x1 |
| 1 |
| 2 |
| (n-1)x1+2 |
| 2x1 |
| 2x1 |
| (n-1)x1+2 |
∵f(x1)=
| 2 |
| 2013 |
| 2x1 |
| x1+2 |
| 2 |
| 2013 |
| 1 |
| 1006 |
∴xn=
2×
| ||
(n-1)•
|
| 2 |
| n+2011 |
| 2 |
| 2015+2011 |
| 1 |
| 2013 |
(3)证明:∵xn=
| 2 |
| n+2011 |
| n+2011 |
| 2 |
∴bn=
| an+12+an2 |
| 2an+1an |
| (2n+1)2+(2n-1)2 |
| 2(2n+1)(2n-1) |
=
| 4n2+1 |
| 4n2-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴b1+b2+…+bn-n
=(1+1-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=1-
| 1 |
| 2n+1 |
故b1+b2+…+bn<n+1.
点评:本题考查函数的表达式的求法,考查数列的第2005项的求法,考查不等式的证明,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
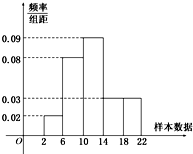 如图是学校从走读生中随机调查200名走读生早上上学所需时间(单位:分钟)样本的频率分布直方图.
如图是学校从走读生中随机调查200名走读生早上上学所需时间(单位:分钟)样本的频率分布直方图.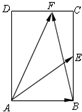 如图,在矩形ABCD中,AB=2,BC=2
如图,在矩形ABCD中,AB=2,BC=2