题目内容
5.已知函数f(x)=sinx-cosx,g(x)=sin2x(1)试说明由函数y=g(x)的图象经过变换得到函数y=f(x)的图象的变换过程;
(2)若h(x)=f(x)+g(x),求函数h(x)的值域.
分析 (1)由已知可得$f(x)=\sqrt{2}sin({x-\frac{π}{4}})$,由函数y=Asin(ωx+φ)的图象变换规律即可得解.
(2)令sinx-cosx=t,则可求sin2x=1-t2,可得h(x)=f(x)+g(x)=φ(t)=-t2+t+1,由t的范围,结合二次函数的性质可求值域.
解答 (本题满分为12分)
解:(1)$f(x)=\sqrt{2}sin({x-\frac{π}{4}})$…(2分)
故先将y=sin2x的图象上所有点纵坐标不变,横坐标伸长到原来的两倍得到y=sinx的图象,
再将y=sinx的图象上所有点横坐标不变,纵坐标伸长到原来的$\sqrt{2}$倍得到$y=\sqrt{2}sinx$的图象,
再把所得图象向左平移$\frac{π}{4}$个单位,即得到$y=\sqrt{2}sin({x-\frac{π}{4}})$的图象.…(5分)
(2)令sinx-cosx=t,则1-2sinxcosx=t2
故sin2x=1-t2
故h(x)=f(x)+g(x)=φ(t)=-t2+t+1…(7分)
由(1)知,$t∈[{-\sqrt{2},\sqrt{2}}],所以φ(t)在[{-\sqrt{2},\frac{1}{2}}]递增,[{\frac{1}{2},\sqrt{2}}]递减$,
所以$φ(t)∈[{-\sqrt{2}-1,\frac{5}{4}}]$,故h(x)的值域为$[{-\sqrt{2}-1,\frac{5}{4}}]$….(12分)
点评 本题值域考查了函数y=Asin(ωx+φ)的图象变换,二次函数的图象和性质的综合应用,考查了转化思想和数形结合思想,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
12.某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )
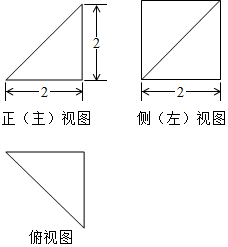

| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2 |
16.甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )
| A. | 乙可以知道四人的成绩 | B. | 丁可以知道四人的成绩 | ||
| C. | 乙、丁可以知道对方的成绩 | D. | 乙、丁可以知道自己的成绩 |
15.设函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,|φ|<π.若f($\frac{5π}{8}$)=2,f($\frac{11π}{8}$)=0,且f(x)的最小正周期大于2π,则( )
| A. | ω=$\frac{2}{3}$,φ=$\frac{π}{12}$ | B. | ω=$\frac{2}{3}$,φ=-$\frac{11π}{12}$ | C. | ω=$\frac{1}{3}$,φ=-$\frac{11π}{24}$ | D. | ω=$\frac{1}{3}$,φ=$\frac{7π}{24}$ |
 如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.