题目内容
11. 如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.求证:(1)EF∥平面ABC;
(2)AD⊥AC.
分析 (1)利用AB∥EF及线面平行判定定理可得结论;
(2)通过取线段CD上点G,连结FG、EG使得FG∥BC,则EG∥AC,利用线面垂直的性质定理可知FG⊥AD,结合线面垂直的判定定理可知AD⊥平面EFG,从而可得结论.
解答 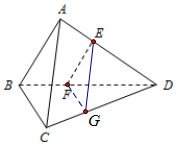 证明:(1)因为AB⊥AD,EF⊥AD,且A、B、E、F四点共面,
证明:(1)因为AB⊥AD,EF⊥AD,且A、B、E、F四点共面,
所以AB∥EF,
又因为EF?平面ABC,AB⊆平面ABC,
所以由线面平行判定定理可知:EF∥平面ABC;
(2)在线段CD上取点G,连结FG、EG使得FG∥BC,则EG∥AC,
因为BC⊥BD,FG∥BC,
所以FG⊥BD,
又因为平面ABD⊥平面BCD,
所以FG⊥平面ABD,所以FG⊥AD,
又因为AD⊥EF,且EF∩FG=F,
所以AD⊥平面EFG,所以AD⊥EG,
故AD⊥AC.
点评 本题考查线面平行及线线垂直的判定,考查空间想象能力,考查转化思想,涉及线面平行判定定理,线面垂直的性质及判定定理,注意解题方法的积累,属于中档题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
1.复数z满足$z({\sqrt{3}+i})=1-\sqrt{3}i$,则|z|=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
2.(x+y)(2x-y)5的展开式中的x3y3系数为 ( )
| A. | -80 | B. | -40 | C. | 40 | D. | 80 |
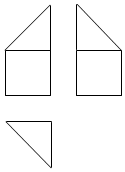 某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )
某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( ) 如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.