题目内容
15.设函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,|φ|<π.若f($\frac{5π}{8}$)=2,f($\frac{11π}{8}$)=0,且f(x)的最小正周期大于2π,则( )| A. | ω=$\frac{2}{3}$,φ=$\frac{π}{12}$ | B. | ω=$\frac{2}{3}$,φ=-$\frac{11π}{12}$ | C. | ω=$\frac{1}{3}$,φ=-$\frac{11π}{24}$ | D. | ω=$\frac{1}{3}$,φ=$\frac{7π}{24}$ |
分析 由题意求得$\frac{T}{4}$,再由周期公式求得ω,最后由若f($\frac{5π}{8}$)=2求得φ值.
解答 解:由f(x)的最小正周期大于2π,得$\frac{T}{4}$$>\frac{π}{2}$,
又f($\frac{5π}{8}$)=2,f($\frac{11π}{8}$)=0,得$\frac{T}{4}=\frac{11π}{8}-\frac{5π}{8}=\frac{3π}{4}$,
∴T=3π,则$\frac{2π}{ω}=3π$,即$ω=\frac{2}{3}$.
∴f(x)=2sin(ωx+φ)=2sin($\frac{2}{3}$x+φ),
由f($\frac{5π}{8}$)=$2sin(\frac{2}{3}×\frac{5π}{8}+φ)=2$,得sin(φ+$\frac{5π}{12}$)=1.
∴φ+$\frac{5π}{12}$=$\frac{π}{2}+2kπ$,k∈Z.
取k=0,得φ=$\frac{π}{12}$<π.
∴$ω=\frac{2}{3}$,φ=$\frac{π}{12}$.
故选:A.
点评 本题考查由三角函数的部分图象求解析式,考查y=Asin(ωx+φ)型函数的性质,是中档题.

练习册系列答案
相关题目
10.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x+y≥0}\\{x+2y-2≥0}\\{x≤0}\\{y≤3}\end{array}\right.$,则目标函数z=x+y的最大值为( )
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 3 |
3.已知f(x)=ln(e2x+1)+xcos2x,则f($\frac{π}{3}$)-f(-$\frac{π}{3}$)=( )
| A. | 0 | B. | $\frac{π}{3}$ | C. | π | D. | $\frac{4π}{3}$ |
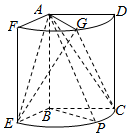 如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.
如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.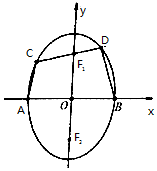 已知F1、F2分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上,下焦点,A,B分别为椭圆的左、右顶点,过椭圆的上焦点F1的直线在x轴上方部分交椭圆于C、D两点,△F2CD的周长为8,若椭圆的离心率为$\frac{\sqrt{3}}{2}$.
已知F1、F2分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上,下焦点,A,B分别为椭圆的左、右顶点,过椭圆的上焦点F1的直线在x轴上方部分交椭圆于C、D两点,△F2CD的周长为8,若椭圆的离心率为$\frac{\sqrt{3}}{2}$.