某四棱锥的三视图如图所示.则该四棱锥的最长棱的长度为( )A．3$\sqrt{2}$B．2$\sqrt{3}$C．2$\sqrt{2}$D．2 题目和参考答案——青夏教育精英家教网—

题目内容

12．某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为（　　）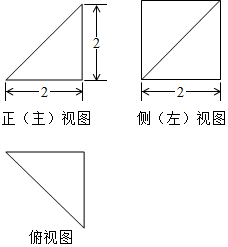

A．

3$\sqrt{2}$

B．

2$\sqrt{3}$

C．

2$\sqrt{2}$

D．

分析根据三视图可得物体的直观图，结合图形可得最长的棱为PA，根据勾股定理求出即可．

解答解：由三视图可得直观图，
再四棱锥P-ABCD中，
最长的棱为PA，
即PA=$\sqrt{P{B}^{2}+P{C}^{2}}$=$\sqrt{{2}^{2}+（2\sqrt{2}）^{2}}$
=2$\sqrt{3}$，
故选：B．

点评本题考查了三视图的问题，关键画出物体的直观图，属于基础题．

练习册系列答案

相关题目

2．（x+y）（2x-y）⁵的展开式中的x³y³系数为（　　）

3．

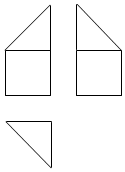某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（　　）

20．

如图，在三棱锥P-ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．
（1）求证：PA⊥BD；
（2）求证：平面BDE⊥平面PAC；
（3）当PA∥平面BDE时，求三棱锥E-BCD的体积．

7．已知函数f（x）=x²-2x+a（e^x-1+e^-x+1）有唯一零点，则a=（　　）

17．

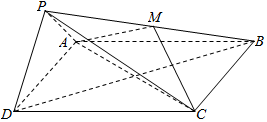如图，在四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD∥平面MAC，PA=PD=$\sqrt{6}$，AB=4．
（1）求证：M为PB的中点；
（2）求二面角B-PD-A的大小；
（3）求直线MC与平面BDP所成角的正弦值．

4．安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有（　　）

5．已知函数f（x）=sinx-cosx，g（x）=sin2x
（1）试说明由函数y=g（x）的图象经过变换得到函数y=f（x）的图象的变换过程；
（2）若h（x）=f（x）+g（x），求函数h（x）的值域．

6．在极坐标系中，点A在圆ρ²-2ρcosθ-4ρsinθ+4=0上，点P的坐标为（1，0），则|AP|的最小值为1．

试题分类