题目内容
19.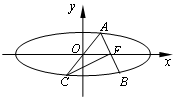 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点为F,过F的直线交椭圆于A,B两点,点C是点A关于原点O的对称点,若CF⊥AB且CF=AB,则椭圆的离心率为$\sqrt{6}-\sqrt{3}$.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点为F,过F的直线交椭圆于A,B两点,点C是点A关于原点O的对称点,若CF⊥AB且CF=AB,则椭圆的离心率为$\sqrt{6}-\sqrt{3}$.
分析 作另一焦点F′,连接AF′和BF′和CF′,则四边形FAF′C为平行四边形,进一步得到三角形ABF′为等腰直角三角形,设AF′=AB=x,求出x,在三角形AFF′中由勾股定理得(AF′)2+(AF)2=(2c)2,即可求出e2,则答案可求.
解答 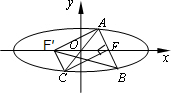 解:作另一焦点F′,连接AF′和BF′和CF′,则四边形FAF′C为平行四边形,
解:作另一焦点F′,连接AF′和BF′和CF′,则四边形FAF′C为平行四边形,
∴AF′=CF=AB,且AF′⊥AB,则三角形ABF′为等腰直角三角形,
设AF′=AB=x,则$x+x+\sqrt{2}x=4a$,即$x=(4-2\sqrt{2})a$,
∴$AF=(2\sqrt{2}-2)a$,在三角形AFF′中由勾股定理得(AF′)2+(AF)2=(2c)2,
∴${e}^{2}=9-6\sqrt{2}$.则e=$\sqrt{6}-\sqrt{3}$.
故答案为:$\sqrt{6}-\sqrt{3}$.
点评 本题考查了椭圆的简单性质,考查了勾股定理在解题中的应用,是中档题.

练习册系列答案
相关题目
9.2016年下半年,锦阳市教体局举行了市教育系统直属单位职工篮球比赛,以增强直属单位间的交流与合作,组织方统计了来自A1,A2,A3,A4,A5等5个直属单位的男子篮球队的平均身高与本次比赛的平均得分,如表所示:
(1)根据表中数据,求y关于x的线性回归方程;(系数精确到0.01)
(2)若M队平均身高为185cm,根据(I)中所求得的回归方程,预测M队的平均得分(精确到0.01)
注:回归当初$\widehat{y}=\widehat{b}x+\widehat{a}$中斜率和截距最小二乘估计公式分别为$\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$.
| 单位 | A1 | A2 | A3 | A4 | A5 |
| 平均身高x(单位:cm) | 170 | 174 | 176 | 181 | 179 |
| 平均得分y | 62 | 64 | 66 | 70 | 68 |
(2)若M队平均身高为185cm,根据(I)中所求得的回归方程,预测M队的平均得分(精确到0.01)
注:回归当初$\widehat{y}=\widehat{b}x+\widehat{a}$中斜率和截距最小二乘估计公式分别为$\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$.
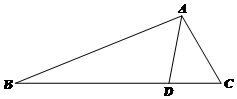 如图,在△ABC中,D是BC上的点,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.
如图,在△ABC中,D是BC上的点,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.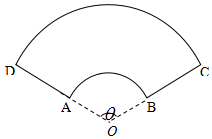 某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).
某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).