题目内容
18. 如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,若$∠{A_1}AB=∠{A_1}AD={60^0}$,且A1A=3,则A1C的长为$\sqrt{17}$.
如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,若$∠{A_1}AB=∠{A_1}AD={60^0}$,且A1A=3,则A1C的长为$\sqrt{17}$.
分析 由$\overrightarrow{{A}_{1}C}$=$\overrightarrow{{A}_{1}A}+\overrightarrow{AB}+\overrightarrow{BC}$,利用向量法能求出A1C的长.
解答 解:在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,
$∠{A_1}AB=∠{A_1}AD={60^0}$,且A1A=3,
$\overrightarrow{{A}_{1}C}$=$\overrightarrow{{A}_{1}A}+\overrightarrow{AB}+\overrightarrow{BC}$,
∴$\overrightarrow{{A}_{1}C}$2=${\overrightarrow{{A}_{1}A}}^{2}$+${\overrightarrow{AB}}^{2}$+${\overrightarrow{BC}}^{2}$+2$\overrightarrow{{A}_{1}A}•\overrightarrow{AB}$+2$\overrightarrow{{A}_{1}A}•\overrightarrow{BC}$
=9+4+4+2×3×2×cos120°+2×3×2×cos60°=17,
∴A1C的长为$\sqrt{17}$.
故答案为:$\sqrt{17}$.
点评 本题考查线段长的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.一个几何体的三视图如图所示,那么该几何体是( )


| A. | 三棱锥 | B. | 四棱锥 | C. | 三棱柱 | D. | 四棱柱 |
9.2016年下半年,锦阳市教体局举行了市教育系统直属单位职工篮球比赛,以增强直属单位间的交流与合作,组织方统计了来自A1,A2,A3,A4,A5等5个直属单位的男子篮球队的平均身高与本次比赛的平均得分,如表所示:
(1)根据表中数据,求y关于x的线性回归方程;(系数精确到0.01)
(2)若M队平均身高为185cm,根据(I)中所求得的回归方程,预测M队的平均得分(精确到0.01)
注:回归当初$\widehat{y}=\widehat{b}x+\widehat{a}$中斜率和截距最小二乘估计公式分别为$\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$.
| 单位 | A1 | A2 | A3 | A4 | A5 |
| 平均身高x(单位:cm) | 170 | 174 | 176 | 181 | 179 |
| 平均得分y | 62 | 64 | 66 | 70 | 68 |
(2)若M队平均身高为185cm,根据(I)中所求得的回归方程,预测M队的平均得分(精确到0.01)
注:回归当初$\widehat{y}=\widehat{b}x+\widehat{a}$中斜率和截距最小二乘估计公式分别为$\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$.
3.己知函数 $f(x)=\frac{x-1}{x}$(其中$x∈[{\frac{1}{2},2}]$)的值域为( )
| A. | $[{-1,\frac{1}{2}}]$ | B. | [-1,2] | C. | $[{\frac{1}{2},2}]$ | D. | $[{\frac{1}{2},1}]$ |
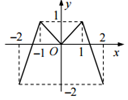 如图,定义在[-2,2]的偶函数f(x)的图象如图所示,函数g(x)=f(x)-$\frac{1}{4}x+\frac{1}{2}$的零点个数为( )
如图,定义在[-2,2]的偶函数f(x)的图象如图所示,函数g(x)=f(x)-$\frac{1}{4}x+\frac{1}{2}$的零点个数为( )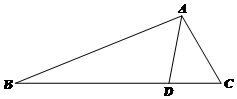 如图,在△ABC中,D是BC上的点,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.
如图,在△ABC中,D是BC上的点,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.