题目内容
2．已知函数f（x）=$\left\{\begin{array}{l}{-x+a，x＜1}\\{{x}^{2}，x≥1}\end{array}\right.$存在最小值，则当实数a取最小值时，f[f（-2）]=（ ）| A． | -2 | B． | 4 | C． | 9 | D． | 16 |
分析 函数f（x）=$\left\{\begin{array}{l}{-x+a，x＜1}\\{{x}^{2}，x≥1}\end{array}\right.$存在最小值，可得-1+a≥12，解得a≥2．再利用分段函数的性质即可得出．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{-x+a，x＜1}\\{{x}^{2}，x≥1}\end{array}\right.$存在最小值，∴-1+a≥12，解得a≥2．
则当实数a取最小值2时，
x＜1时，f（x）=-x+2．
∴f（-2）=4．
f[f（-2）]=f（4）=42=16．
故选：D．
点评 本题考查了分段函数的性质及其应用、不等式的解法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
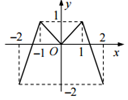如图，定义在[-2，2]的偶函数f（x）的图象如图所示，函数g（x）=f（x）-$\frac{1}{4}x+\frac{1}{2}$的零点个数为（ ）
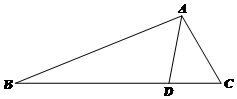如图，在△ABC中，D是BC上的点，AC=3，CD=2，AD=$\sqrt{7}$，sinB=$\frac{\sqrt{7}}{7}$．
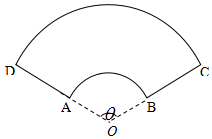某公司拟设计一个扇环形状的花坛（如图所示），该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成．设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f（x）、R米，圆心角为θ（弧度）．
14．从5名男同学，4名女同学中任选5人参加一次夏令营，其中男同学，女同学均不少于2人的概率是（ ）
| A． | $\frac{13}{63}$ | B． | $\frac{50}{63}$ | C． | $\frac{43}{63}$ | D． | $\frac{11}{63}$ |