题目内容
16.已知点A(-1,0,1),B(0,0,1),C(2,2,2),D(0,0,3),则向量$\overrightarrow{AB}$与$\overrightarrow{CD}$的夹角的余弦值为-$\frac{2}{3}$.分析 先求出向量$\overrightarrow{AB}$,$\overrightarrow{CD}$,利用cos<$\overrightarrow{AB},\overrightarrow{CD}$>=$\frac{\overrightarrow{AB}•\overrightarrow{CD}}{|\overrightarrow{AB}|•|\overrightarrow{CD}|}$,能求出向量$\overrightarrow{AB}$与$\overrightarrow{CD}$的夹角的余弦值.
解答 解:∵点A(-1,0,1),B(0,0,1),C(2,2,2),D(0,0,3),
∴$\overrightarrow{AB}$=(1,0,0),$\overrightarrow{CD}$=(-2,-2,1),
∴cos<$\overrightarrow{AB},\overrightarrow{CD}$>=$\frac{\overrightarrow{AB}•\overrightarrow{CD}}{|\overrightarrow{AB}|•|\overrightarrow{CD}|}$=$\frac{-2}{1×\sqrt{9}}$=-$\frac{2}{3}$.
∴向量$\overrightarrow{AB}$与$\overrightarrow{CD}$的夹角的余弦值为-$\frac{2}{3}$.
点评 本题考查向量夹角的余弦值的求法,考查空间向量坐标运算法则、空间向量夹角余弦值计算公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
4.已知函数f(x)定义域为R,命题p:?x1,x2∈R,(f(x1)-f(x2))(x1-x2)<0,则¬p是( )
| A. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)>0 | B. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)≥0 | ||
| C. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)≥0 | D. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)<0 |
11.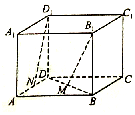 如图所示,在正方体ABCD-A1B1C1D1中,已知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,已知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
 如图所示,在正方体ABCD-A1B1C1D1中,已知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,已知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )| A. | $\frac{\sqrt{30}}{10}$ | B. | $\frac{\sqrt{30}}{10}$a | C. | -$\frac{\sqrt{30}}{10}$ | D. | $\frac{\sqrt{15}}{15}$a |
1.正数a、m、b构成公差为-$\frac{1}{2}$的等差数列,a,b的等比中项是2$\sqrt{5}$,则双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{\sqrt{41}}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{\sqrt{41}}{5}$ |
9.已知点A,B,C在圆x2+y2=4上运动,且AB⊥BC.若点P的坐标为(3,4),则$|{\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}}|$的取值范围为( )
| A. | [10,15] | B. | [12,17] | C. | [13,17] | D. | [15,17] |