题目内容
某厂2013年、2014年某产品的生产量分别为1000件、1050件,由于技术条件的改进,该产品的年产量逐年递增.若用函数f(x)=a•bx+c(b>0,且b≠1)模拟该产品的年生产量f(x)与年份x(x∈N*)的关系,设2013年为第一年即x=1.
(1)若b=
,试求函数f(x)的解析式;
(2)若b>1,由于生产规模的限制,估计2015年该产品的生产量不会突破1200件(即生产量≤1200件),试依此估计求出a的取值范围.
(1)若b=
| 1 |
| 2 |
(2)若b>1,由于生产规模的限制,估计2015年该产品的生产量不会突破1200件(即生产量≤1200件),试依此估计求出a的取值范围.
考点:函数模型的选择与应用,函数解析式的求解及常用方法
专题:应用题,函数的性质及应用
分析:(1)利用厂2013年、2014年某产品的生产量分别为1000件、1050件,建立方程组,求出a,c,即可求函数f(x)的解析式;
(2)由题意,
,可得a=
,c=1000-ab,结合2015年该产品的生产量不会突破1200件(即生产量≤1200件),可得ab3+c≤1200,确定b的范围,即可求出a的取值范围.
(2)由题意,
|
| 50 |
| b2-b |
解答:
解:(1)由题意,
,∴a=-200,c=1100,
∴f(x)=-200(
)x+1100(x∈N*);(6分)
(2)由题意,
,
∴a=
,c=1000-ab
∵2015年该产品的生产量不会突破1200件(即生产量≤1200件),
∴ab3+c≤1200
∴ab3-ab≤200,
∴
×(b3-b)≤200,
∴b≤3,
∵b>1,
∴0<b2-b≤6
∴a=
≥
,即a∈[
,+∞).(10分)
|
∴f(x)=-200(
| 1 |
| 2 |
(2)由题意,
|
∴a=
| 50 |
| b2-b |
∵2015年该产品的生产量不会突破1200件(即生产量≤1200件),
∴ab3+c≤1200
∴ab3-ab≤200,
∴
| 50 |
| b2-b |
∴b≤3,
∵b>1,
∴0<b2-b≤6
∴a=
| 50 |
| b2-b |
| 25 |
| 3 |
| 25 |
| 3 |
点评:本题考查函数模型的运用,考查利用数学知识解决实际问题,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
命题“?x∈(0,+∞),x+
≥4”的否定为( )
| 4 |
| x |
A、?x∈(0,+∞),x+
| ||
B、?x∈(0,+∞),x+
| ||
C、?x∈(0,+∞),x+
| ||
D、?x∈(0,+∞),x+
|
若命题p:2是偶数,命题q:2是3的约数,则下列结论中正确的是( )
| A、“p∨q”为假 |
| B、“p∨q”为真 |
| C、“p∧q”为真 |
| D、以上都不对 |
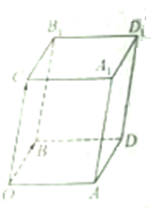 如图,已知向量
如图,已知向量