题目内容
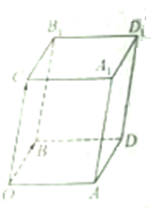如图，已知向量| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| a |
| b |
（1）求证：向量
| p |
（2）求证：以OA，OB为边的平行四边形OADB的面积等于|
| a |
| b |
（3）将四边形OADB按向量c平移，得到一个平行六面体OADB-CA1D1B1，是判断平行六面体的体积V与（
| a |
| b |
| c |
考点：空间向量的数量积运算
专题：空间向量及应用
分析：（1）由题意，得
⊥
，
⊥
，由此能证明
为平面OAB的法向量．
（2）设
，
夹角为θ，
•
=|
|•|
|cosθ=a1b1+a2b2+a3b3，SOABD2=（|
||
|sinθ）2，由此能证明SOABD=|
×
|．
（3）（
×
）•
=
向量在面OAB法向量上的投影×|
|，
=
×
的几何意义是|
|=|
|•|
|•sin＜
，
＞，由此能求出V=|（
×
）•
|．
| p |
| a |
| p |
| b |
| p |
（2）设
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
（3）（
| a |
| b |
| c |
| OC |
| p |
| p |
| a |
| b |
| p |
| a |
| b |
| a |
| b |
| a |
| b |
| c |
解答：
（1）证明：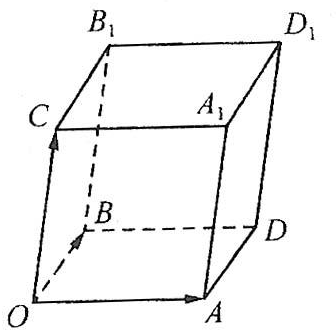
由题意，得
•
=（a1a2b3-a1a3b2，a2a3b1-a1a2b3，a1b2a3-a2b1b3），
因为（a1a2b3-a1a3b2）+（a2a3b1-a1a2b3）+（a1b2a3-a2b1b3）=0，
所以
⊥
，
同理得
⊥
，
因为
⊥
，且
，
?平面OAB，
所以
为平面OAB的法向量．
（2）证明：设
，
夹角为θ，
•
=|
|•|
|cosθ=a1b1+a2b2+a3b3，
SOABD2=（|
||
|sinθ）2
=|
|2|
|2（1-cos2θ）
=|
|2|
|2-|
|2|
|2cos2θ
=（
×
）2
所以SOABD=|
×
|．
（3）（
×
）•
=
向量在面OAB法向量上的投影×|
|，
=
×
的几何意义是|
|=|
|•|
|•sin＜
，
＞，
∴|
|是底面积，
∴V=|
|•
在法向量上投影
=|（
×
）•
|．
由题意，得| p |
| a |
因为（a1a2b3-a1a3b2）+（a2a3b1-a1a2b3）+（a1b2a3-a2b1b3）=0，
所以
| p |
| a |
同理得
| p |
| b |
因为
| a |
| b |
| a |
| b |
所以
| p |
（2）证明：设
| a |
| b |
| a |
| b |
| a |
| b |
SOABD2=（|
| a |
| b |
=|
| a |
| b |
=|
| a |
| b |
| a |
| b |
=（
| a |
| b |
所以SOABD=|
| a |
| b |
（3）（
| a |
| b |
| c |
| OC |
| p |
| p |
| a |
| b |
| p |
| a |
| b |
| a |
| b |
∴|
| p |
∴V=|
| p |
| OC |
=|（
| a |
| b |
| c |
点评：本题考查向量
为平面OAB的法向量的证明，考查以OA，OB为边的平行四边形OADB的面积等于|
×
|的证明，考查平行六面体的体积V与（
×
）•
的大小的判断，解题时要注意向量的数量积的合理运用．
| p |
| a |
| b |
| a |
| b |
| c |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
复数z满足方程|z+
|=4，那么复数z在复平面内对应的点P组成的图形为（ ）
| 2 |
| 1+i |
| A、以（1，-1）为圆心，以4为半径的圆 |
| B、以（1，-1）为圆心，以2为半径的圆 |
| C、以（-1，1）为圆心，以4为半径的圆 |
| D、以（-1，1）为圆心，以2为半径的圆 |
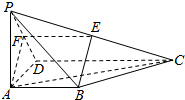如图，四棱锥P-ABCD，PA⊥底面ABCD，AB∥CD，AB⊥AD，AB=AD=PA=2，CD=4，E，F分别是PC，PD的中点．
如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD的边BC垂直于圆O所在的平面．
用黑、蓝2种颜色给如图所示的笑脸涂色，每个图形只能涂一种颜色，则两只眼睛（即图中A、B所示的区域）涂同种颜色而鼻子和嘴巴涂不同颜色的概率为