题目内容
已知函数f(x)=ex(e=2.71828…是自然对数的底数),x∈R.
(Ⅰ)求函数y=f(x)的图象过原点的切线方程;
(Ⅱ)设x>0,讨论曲线y=f(x)与曲线y=mx2(m>0)公共点的个数;
(Ⅲ)设a<b,证明
>
.
(Ⅰ)求函数y=f(x)的图象过原点的切线方程;
(Ⅱ)设x>0,讨论曲线y=f(x)与曲线y=mx2(m>0)公共点的个数;
(Ⅲ)设a<b,证明
| f(a)+f(b) |
| 2 |
| f(b)-f(a) |
| b-a |
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(I)先求出其反函数,利用导数得出切线的斜率即可;
(II)由f(x)=mx2,令h(x)=
(x>0),利用导数研究函数h(x)的单调性即可得出;
(III)利用作差法
>
=
ea,令g(x)=x+2+(x-2)ex(x>0),利用导数研究其单调性即可证明.
(II)由f(x)=mx2,令h(x)=
| ex |
| x2 |
(III)利用作差法
| f(a)+f(b) |
| 2 |
| f(b)-f(a) |
| b-a |
| (b-a+2)+(b-a-2)eb-a |
| 2(b-a) |
解答:
(Ⅰ)解:设切线方程为y=kx,切点为(x0,y0),则
∴x0=1,k=e,
∴函数y=f(x)的图象过原点的切线方程为y=ex;
(Ⅱ)解:当x>0,m>0时,令f(x)=mx2,化为m=
,
令h(x)=
(x>0),则h′(x)=
,
则x∈(0,2)时,h′(x)<0,h(x)单调递减;x∈(2,+∞)时,h′(x)>0,h(x)单调递增.
∴当x=2时,h(x)取得极小值即最小值,h(2)=
.
∴当m∈(0,
)时,曲线y=f (x) 与曲线y=mx2(m>0)公共点的个数为0;
当m=
时,曲线y=f (x) 与曲线y=mx2(m>0)公共点的个数为1;
当m>
时,曲线y=f (x) 与曲线y=mx2(m>0)公共点个数为2.
(Ⅲ)证明:
>
=
ea,
令g(x)=x+2+(x-2)ex(x>0),则g′(x)=1+(x-1)ex.
g′′(x)=xex>0,∴g′(x)在(0,+∞)上单调递增,且g′(0)=0,
∴g′(x)>0,∴g(x)在(0,+∞)上单调递增,
而g(0)=0,∴在(0,+∞)上,有g(x)>g(0)=0.
∵当x>0时,g(x)=x+2+(x-2)•ex>0,且a<b,
∴
ea>0,
即当a<b时,
>
.
|
∴x0=1,k=e,
∴函数y=f(x)的图象过原点的切线方程为y=ex;
(Ⅱ)解:当x>0,m>0时,令f(x)=mx2,化为m=
| ex |
| x2 |
令h(x)=
| ex |
| x2 |
| ex(x-2) |
| x3 |
则x∈(0,2)时,h′(x)<0,h(x)单调递减;x∈(2,+∞)时,h′(x)>0,h(x)单调递增.
∴当x=2时,h(x)取得极小值即最小值,h(2)=
| e2 |
| 4 |
∴当m∈(0,
| e2 |
| 4 |
当m=
| e2 |
| 4 |
当m>
| e2 |
| 4 |
(Ⅲ)证明:
| f(a)+f(b) |
| 2 |
| f(b)-f(a) |
| b-a |
| (b-a+2)+(b-a-2)eb-a |
| 2(b-a) |
令g(x)=x+2+(x-2)ex(x>0),则g′(x)=1+(x-1)ex.
g′′(x)=xex>0,∴g′(x)在(0,+∞)上单调递增,且g′(0)=0,
∴g′(x)>0,∴g(x)在(0,+∞)上单调递增,
而g(0)=0,∴在(0,+∞)上,有g(x)>g(0)=0.
∵当x>0时,g(x)=x+2+(x-2)•ex>0,且a<b,
∴
| (b-a+2)+(b-a-2)eb-a |
| 2(b-a) |
即当a<b时,
| f(a)+f(b) |
| 2 |
| f(b)-f(a) |
| b-a |
点评:本题综合考查了利用导数研究切线、单调性、方程得根的个数、比较两个实数的大小等基础知识,考查了分类讨论的思想方法、转化与化归思想方法,考查了推理能力和计算能力.

练习册系列答案
相关题目
已知△ABC中,平面内一点P满足
=
+
,若|
|=t|
|,则t的值为( )
| CP |
| 2 |
| 3 |
| CA |
| 1 |
| 3 |
| CB |
| PB |
| PA |
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
如图所示,程序框图(算法流程图)的输出结果是( )
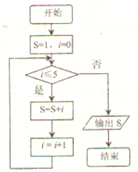

| A、11 | B、15 | C、16 | D、22 |
已知四棱锥P-ABCD,现要在四棱锥的各个面上涂色,有4种不同的颜色可供选择,要求相邻的面不同色,则不同的涂色方法有( )种.
| A、60 | B、120 | C、48 | D、72 |
设{an}的首项为a1,公差为-1的等差数列,Sn为其前n项和,若S1,S2,S4成等比数列,则a1=( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|