题目内容
6.若直线y=2x上存在点(x,y)满足条件$\left\{\begin{array}{l}x+y-3≤0\\ x-2y-3≥0\\ x≥m.\end{array}\right.$,则实数m的最大值为( )| A. | -2 | B. | -1 | C. | 1 | D. | 3 |
分析 作出约束条件中的前两个不等式表示的平面区域,求解直线y=2x与直线x-2y-3=0的交点,得到交点的横坐标,结合直线y=2x上存在点(x,y)满足条件$\left\{\begin{array}{l}x+y-3≤0\\ x-2y-3≥0\\ x≥m.\end{array}\right.$,即可得到实数m的最大值.
解答 解:如图,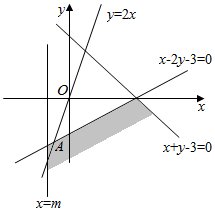
在坐标平面内画出二元一次不等式x+y-3≤0,x-2y-3≥0所表示的平面区域,
求出直线y=2x与直线x-2y-3=0的交点A(-1,-2),
由图可知,要使直线y=2x上存在点(x,y)满足条件$\left\{\begin{array}{l}x+y-3≤0\\ x-2y-3≥0\\ x≥m.\end{array}\right.$,则m≤-1.
即实数m的最大值为-1.
故答案为:-1.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
16.若关于x的方程3x=$\frac{a+3}{5-a}$无负数根,则a的取值范围为( )
| A. | a≥1 | B. | a<5 | C. | (-∞,1]∪(5,+∞) | D. | [1,5) |
11.已知$\frac{zi}{i-1}=i+1$,则复数z在复平面上所对应的点位于( )
| A. | 实轴上 | B. | 虚轴上 | C. | 第一象限 | D. | 第二象限 |
18.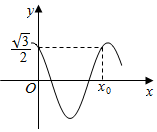 已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=f(0),则正确的选项是( )
已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=f(0),则正确的选项是( )
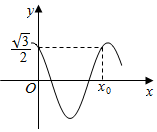 已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=f(0),则正确的选项是( )
已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=f(0),则正确的选项是( )| A. | $φ=\frac{π}{6},{x_0}=\frac{5}{3}$ | B. | $φ=\frac{π}{6},{x_0}=1$ | C. | $φ=\frac{π}{3},{x_0}=\frac{5}{3}$ | D. | $φ=\frac{π}{3},{x_0}=1$ |
16.若随机变量Y~B(5,$\frac{1}{4}$),则EY为( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{5}{4}$ | D. | -$\frac{5}{4}$ |
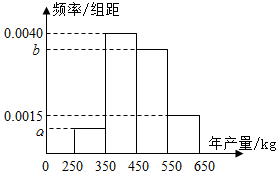 某人租用一块土地种植一种瓜类作物,租期5年,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg时,单位售价为10元/kg.
某人租用一块土地种植一种瓜类作物,租期5年,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg时,单位售价为10元/kg.