题目内容
18.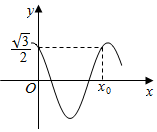 已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=f(0),则正确的选项是( )
已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=f(0),则正确的选项是( )| A. | $φ=\frac{π}{6},{x_0}=\frac{5}{3}$ | B. | $φ=\frac{π}{6},{x_0}=1$ | C. | $φ=\frac{π}{3},{x_0}=\frac{5}{3}$ | D. | $φ=\frac{π}{3},{x_0}=1$ |
分析 根据函数f(x)的部分图象知f(0)=$\frac{\sqrt{3}}{2}$,分别验证A、B、C、D选项是否满足条件即可.
解答 解:根据函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象知,
f(0)=$\frac{\sqrt{3}}{2}$,
对于A,cos($\frac{5}{3}$π+$\frac{π}{6}$)=cos$\frac{11π}{6}$=cos$\frac{π}{6}$=$\frac{\sqrt{3}}{2}$,满足题意;
对于B,cos(π+$\frac{π}{6}$)=-cos$\frac{π}{6}$=-$\frac{\sqrt{3}}{2}$,不满足题意;
对于C,cos($\frac{5}{3}$π+$\frac{π}{3}$)=cos2π=1,不满足题意;
对于D,cos(π+$\frac{π}{3}$)=-cos$\frac{π}{3}$=-$\frac{1}{2}$,不满足题意;
故选:A.
点评 本题考查了函数y=Asin(ωx+φ的图象与应用问题,是基础题目.

练习册系列答案
相关题目
8.已知函数f(x)=1g(x+$\sqrt{{x}^{2}+1}$),若对于任意的x∈(1,2]时,f($\frac{x+1}{x-1}$)+f[$\frac{m}{(x-1)^{2}(x-6)}$]>0恒成立,则实数m的取值范围是( )
| A. | [4,+∞) | B. | (12,+∞) | C. | (-∞,0) | D. | (-∞,0] |
9.若非空集合A,B满足A?B,则“x∈A”是“x∈B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
6.若直线y=2x上存在点(x,y)满足条件$\left\{\begin{array}{l}x+y-3≤0\\ x-2y-3≥0\\ x≥m.\end{array}\right.$,则实数m的最大值为( )
| A. | -2 | B. | -1 | C. | 1 | D. | 3 |
3.已知命题p:函数f(x)=|2cos2x-1|的最小正周期为π;
命题q:若函数f(x-2)为奇函数,则f(x)关于(-2,0)对称,则下列命题是真命题的是( )
命题q:若函数f(x-2)为奇函数,则f(x)关于(-2,0)对称,则下列命题是真命题的是( )
| A. | p∧q | B. | p∨q | C. | (¬p)∧(¬q) | D. | p∧(¬q) |
8.函数f(x)=cos(2π-x)-x3sinx是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数又不是偶函数 |