题目内容
16．若随机变量Y～B（5，$\frac{1}{4}$），则EY为（ ）| A． | $\frac{1}{4}$ | B． | -$\frac{1}{4}$ | C． | $\frac{5}{4}$ | D． | -$\frac{5}{4}$ |
分析 由已知直接利用二项分布的性质求解．
解答 解：∵随机变量Y～B（5，$\frac{1}{4}$），
∴EY=5×$\frac{1}{4}$=$\frac{5}{4}$．
故选：C．
点评 本题考查离散型随机变量的数学期望的求法，是基础题，解题时要注意二项分布的性质的合理运用．
练习册系列答案
相关题目
6．若直线y=2x上存在点（x，y）满足条件$\left\{\begin{array}{l}x+y-3≤0\\ x-2y-3≥0\\ x≥m.\end{array}\right.$，则实数m的最大值为（ ）
| A． | -2 | B． | -1 | C． | 1 | D． | 3 |
4．在等差数列{an}中，a2、a13是方程x2-x-3=0的两个根，则前14项的和S14为（ ）
| A． | 20 | B． | 16 | C． | 12 | D． | 7 |
11．已知向量$\overrightarrow{a}=（\sqrt{3}，1）$，向量$\overrightarrow{b}=（-1，\sqrt{3}）$，则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
1．已知f′（x）是定义在R上的函数f（x）的导数，满足f′（x）+2f（x）＞0，且f（-1）=0，则f（x）＜0的解集为（ ）
| A． | （-∞，-1） | B． | （-1，1） | C． | （-∞，0） | D． | （-1，+∞） |
8．函数f（x）=cos（2π-x）-x3sinx是（ ）
| A． | 奇函数 | B． | 偶函数 | ||
| C． | 既是奇函数又是偶函数 | D． | 既不是奇函数又不是偶函数 |
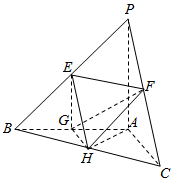如图，在三棱锥P-ABC中，E、F、G、H分别是棱PB、PC、AB、BC的中点，PA⊥平面ABC，AB⊥AC，PA=AB=AC=2．