Question

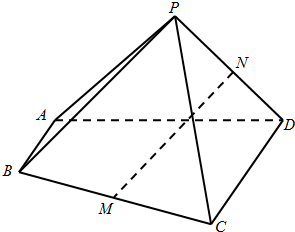
已知正四棱锥P-ABCD棱长都等于a，侧棱PB，PD的中点分别为M，N，则截面AMN与底面ABCD所成锐二面角的正切值为（　　）

• A、

  3

  3

• B、

  1

  2

• C、1
• D、

  2

Answer 1

考点：二面角的平面角及求法

专题：综合题,空间角

分析：证明BD⊥面PAC，过A作直线l∥BD，则l⊥EA，l⊥AO，可得∠EAO为所求二面角的平面角，即可得出结论．

解答： 解：如图，正四棱锥P-ABCD中，O为正方形ABCD的两对角线的交点，则PO⊥面ABCD，PO交MN于E，则PE=EO，
又BD⊥AC，∴BD⊥面PAC，
过A作直线l∥BD，则l⊥EA，l⊥AO，
∴∠EAO为所求二面角的平面角．
又EO=

1

2

AO=

2

4

a，AO=

2

2

a，
∴tan∠EAO=

1

2

．
故选：B．

点评：本题考查二面角的平面角及求法，考查学生分析解决问题的能力，比较基础．