题目内容
已知函数f(x)=ln(ax)-
(a≠0).
(1)求此函数的单调区间及最值;
(2)当a=1时,是否存在过点(-1,1)的直线与函数y=f(x)的图象相切?若存在,有多少条?若不存在,说明理由.
| x-a |
| x |
(1)求此函数的单调区间及最值;
(2)当a=1时,是否存在过点(-1,1)的直线与函数y=f(x)的图象相切?若存在,有多少条?若不存在,说明理由.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程,导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)先求出函数的定义域,再求导,然后分类讨论求出函数的单调区间和最值.
(2)求导数,利用导数的几何意义进行判断.
(2)求导数,利用导数的几何意义进行判断.
解答:
解:(1)∵函数f(x)=ln(ax)-
(a≠0).
∴ax>0
∴f′(x)=
-
=
,
令f′(x)=0,得x=a,
①a>0时,则x>0,函数f(x)在(0,a)上递减,在(a,+∞)上递增,
故当x=a时,函数有最小值,最小值为f(a)=2lna,
②a<0时,则x<0,函数f(x)在(-∞,a)上递减,在(a,0)上递增,
故当x=a时,函数有最小值,最小值为f(a)=2ln(-a),
(2)当a=1时,f(x)=lnx+
-1,(x>0)
∴f′(x)=
-
=
,(x>0),
设切点为T(x0,lnx0+
-1),
∴切线的斜率k=
=
,
∴lnx0+
+
-3=0,①
设g(x)=lnx+
+
-3,
∴g′(x)=
,
令g′(x)=0,解得x=
∵x>0,
∴g(x)在区间(0,
)是减函数,(
,+∞)上是增函数,
∵g(1)=ln1+1+1-3=-1<0,g(
)=ln
+2+4-3=3-ln2>0,
注意到g(x)在其定义域上的单调性,知g(x)=0仅在(
,1)内有且仅有一根
所以方程①有且仅有一解,故符合条件的切线有且仅有一条.
| x-a |
| x |
∴ax>0
∴f′(x)=
| 1 |
| x |
| a |
| x2 |
| x-a |
| x2 |
令f′(x)=0,得x=a,
①a>0时,则x>0,函数f(x)在(0,a)上递减,在(a,+∞)上递增,
故当x=a时,函数有最小值,最小值为f(a)=2lna,
②a<0时,则x<0,函数f(x)在(-∞,a)上递减,在(a,0)上递增,
故当x=a时,函数有最小值,最小值为f(a)=2ln(-a),
(2)当a=1时,f(x)=lnx+
| 1 |
| x |
∴f′(x)=
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x2 |
设切点为T(x0,lnx0+
| 1 |
| x0 |
∴切线的斜率k=
| x0-1 |
| x02 |
lnx0+
| ||
| x0+1 |
∴lnx0+
| 1 |
| x02 |
| 1 |
| x0 |
设g(x)=lnx+
| 1 |
| x |
| 1 |
| x2 |
∴g′(x)=
| x2-x-1 |
| x3 |
令g′(x)=0,解得x=
-1+
| ||
| 2 |
∵x>0,
∴g(x)在区间(0,
-1+
| ||
| 2 |
-1+
| ||
| 2 |
∵g(1)=ln1+1+1-3=-1<0,g(
| 1 |
| 2 |
| 1 |
| 2 |
注意到g(x)在其定义域上的单调性,知g(x)=0仅在(
| 1 |
| 2 |
所以方程①有且仅有一解,故符合条件的切线有且仅有一条.
点评:本题主要考查利用导数研究函数的性质,要求熟练掌握导数和函数单调性,极值之间的关系,考查学生的运算能力

练习册系列答案
相关题目
已知定义域为R的函数f (x)满足对任意的x1,x2∈(8,+∞)(x1<x2),有f(x1)>f(x2),且函数y=f(x+8)为偶函数,则( )
| A、f (6)>f (7) |
| B、f (6)>f (9) |
| C、f (7)>f (9) |
| D、f (7)>f (10) |
已知a,b,c,d是四条不重合的直线,其中c为a在平面α上的射影,d为b在平面α上的射影,则( )
| A、c∥d⇒a∥b |
| B、a⊥b⇒c⊥d |
| C、a∥b⇒c∥d |
| D、c⊥d⇒a⊥b |
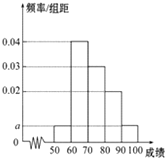 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]